Wiskundeforum

Hallo,

Voor mijn profielwerkstuk wil ik het verband tussen de Riemann zèta functie $\zeta(s)$ en de priemtelfunctie $\pi(x)$ uitleggen. Van de afleiding van een vergelijking snap ik alleen het volgende niet:

Waarom geldt:
$\int_{n}^{n+1}{{s\cdot\pi(n)}\over{x(x^s-1)}}dx=\int_{n}^{n+1}{{s\cdot\pi(x)}\over{x(x^s-1)}}dx$
Het enige wat hier dus verandert is het argument van de priemtelfunctie.

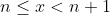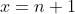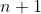Ik snap dat $\pi(x)$ gelijk is voor alle $n\leq x<n+1$ , maar voor $x=n+1$ heeft $\pi(x)$ soms toch wel een andere waarde (namelijk als $n+1$ priem is)?

In een youtube video die ik had gevonden, wordt gezegd dat er niet gekeken wordt naar de grenzen van de integraal. Kan iemand mij misschien uitleggen waarom dit zo is?
Heel erg bedankt alvast!

Edit:
Het kan natuurlijk ook dat die youtube video niet klopt. Zelf verwacht ik eigenlijk van niet, aangezien ik de conclusie van de video, de vergelijking $ln(\zeta(s))=\int_{2}^{\infty}{{s\pi(x)}\over{x(x^s-1)}}dx$ , ook in een paper ergens tegen ben gekomen, waar ik nu helaas de URL niet meer van heb.

De dikte bij dat stukje van de integraal is 0, niet?
met $\int_a^a f(x) d x = 0$ ?

De integraal

$\displaystyle \int_a^b f(x) \; dx$

is gedefinieerd voor functies f continu op het interval [a, b].
(zie bv. https://nl.wikipedia.org/wiki/Integraal ... alrekening)

De integraal

$\displaystyle \int_{n}^{n+1}{{s\cdot\pi(x)}\over{x(x^s-1)}}dx$

is niet gedefinieerd als n+1 priem is, omdat $\pi(x)$ dan niet continu is op het interval [n, n+1].

Maar omdat $\pi(x) = \pi(n) = \text{constant}$ voor $n \le x < n+1$
en de integraal van (n+1) tot (n+1) gelijk is aan nul (zie David hierboven)
valt die stap te verantwoorden.

arie schreef: ↑
20 feb 2020, 10:00
De integraal

$\displaystyle \int_{n}^{n+1}{{s\cdot\pi(x)}\over{x(x^s-1)}}dx$

is niet gedefinieerd als n+1 priem is, omdat $\pi(x)$ dan niet continu is op het interval [n, n+1].

Oh wauw, bedankt! Op school had ik nog niet geleerd dat je niet kan integreren waar de functie niet continu is, dus had hier niet aan gedacht. Maar dat is wel logisch eigenlijk, bedankt.

David schreef: ↑
20 feb 2020, 02:43
De dikte bij dat stukje van de integraal is 0, niet?
met $\int_a^a f(x) d x = 0$ ?

Sorry, maar ik snap eigenlijk niet helemaal wat u hier bedoelt...
Waarschijnlijk heb ik het mis hoor, maar die vergelijking klopt toch altijd, voor elke functie $\displaystyle f(x)$?
Want $\displaystyle \int_{a}^{a}f(x)dx=[F(x)]^a_a=F(a)-F(a)=0$
Alvast bedankt voor uw reactie!

Wiskundeforum

Bovengrens integraal

Bovengrens integraal

Re: Bovengrens integraal

Re: Bovengrens integraal

Re: Bovengrens integraal