Telproblemen & kansrekenen (21-6-2012)
Telproblemen & kansrekenen (21-6-2012)
Hallo
Morgen heb ik examen statistiek en gisteren kregen we nog enkele herhalingsoefeningen.
Nu is het probleem dat ik hier geen modeloplossing heb bij gekregen. Ik heb dus geen tijd om dit oefening per oefening op te lossen op het forum dus doe ik het via deze weg.
Ik ben dus snel naar iemand op zoek die 15 oefeningen ivm telproblemen en kansrekenen tegen vanavond nog voor mij wil oplossen.
Ik wil hier gerust een kleine betaling als tegenprestatie voor doen...
Dit zijn de oefeningen: http://www.mijnbestand.nl/Bestand-ARAW7WXBZKMT.pdf (laatste blad hoeft niet)
Bedankt
Morgen heb ik examen statistiek en gisteren kregen we nog enkele herhalingsoefeningen.
Nu is het probleem dat ik hier geen modeloplossing heb bij gekregen. Ik heb dus geen tijd om dit oefening per oefening op te lossen op het forum dus doe ik het via deze weg.
Ik ben dus snel naar iemand op zoek die 15 oefeningen ivm telproblemen en kansrekenen tegen vanavond nog voor mij wil oplossen.
Ik wil hier gerust een kleine betaling als tegenprestatie voor doen...
Dit zijn de oefeningen: http://www.mijnbestand.nl/Bestand-ARAW7WXBZKMT.pdf (laatste blad hoeft niet)
Bedankt
Laatst gewijzigd door Piden9 op 20 jun 2012, 15:17, 1 keer totaal gewijzigd.
Re: Telproblemen & kansrekenen (vandaag)
Wellicht heeft iemand de antwoorden al.
Kan je een link naar je vragen geven of ze zelf op het web zetten (zie zo nodig
viewtopic.php?f=15&t=5039
hoe je dit kan doen)
Geef daarbij zelf ook s.v.p. je eigen antwoorden aan (en mochten er vragen zijn waar je niet helemaal uit komt: tot hoe ver je gekomen bent). Doorgaans kunnen we je hier dan wel verder helpen.
Kan je een link naar je vragen geven of ze zelf op het web zetten (zie zo nodig
viewtopic.php?f=15&t=5039
hoe je dit kan doen)
Geef daarbij zelf ook s.v.p. je eigen antwoorden aan (en mochten er vragen zijn waar je niet helemaal uit komt: tot hoe ver je gekomen bent). Doorgaans kunnen we je hier dan wel verder helpen.
Re: Telproblemen & kansrekenen (vandaag)
Dit zijn de oefeningen http://www.mijnbestand.nl/Bestand-ARAW7WXBZKMT.pdf laatste blad hoeft niet.
Als je mij al zou kunnen zeggen welke soort van telprobleem ik heb, ben ik er al veel mee. Maar zoals ik al zei, ik heb helaas niet genoeg tijd om steeds te wachten op bevestiging. Daarom zou ik graag iemand betalen voor mijn oefeningen te maken.
Bedankt
Als je mij al zou kunnen zeggen welke soort van telprobleem ik heb, ben ik er al veel mee. Maar zoals ik al zei, ik heb helaas niet genoeg tijd om steeds te wachten op bevestiging. Daarom zou ik graag iemand betalen voor mijn oefeningen te maken.
Bedankt
Re: Telproblemen & kansrekenen (vraag 2)
Wat onduidelijke vraagstelling, ik vermoed dat de 3 jongensfietsen als onderling gelijk gezien worden, en de 5 meisjesfietsen ook. Dit is dan vergelijkbaar met problemen met bv 3 blauwe kralen en 5 rode kralen.
In dat geval:
[2a] kies 3 plaatsen uit 8 plaatsen om de 3 fietsen van de jongens te plaatsen, de overige plaatsen zijn voor de meisjes.
[2b] de fietsen van de jongens vormen samen 1 blok, daarnaast zijn er 5 plaatsen voor de meisjesfietsen. Kies nu 1 plaats uit 6 om de jongensfietsen te plaatsen, de overige zijn voor de meisjes (vergelijk [2a])
[2c] na plaatsing van de meisjesfietsen blijven er 6 plaatsen over waar we 3 jongensfietsen en 3 meisjesfietsen moeten plaatsen. (vergelijk [2a])
[2d] aantal meisjesfietsen met een folder is 0,1,2 of 3, de overige folders gaan naar de jongensfietsen (en dat aantal ligt vast).
In dat geval:
[2a] kies 3 plaatsen uit 8 plaatsen om de 3 fietsen van de jongens te plaatsen, de overige plaatsen zijn voor de meisjes.
[2b] de fietsen van de jongens vormen samen 1 blok, daarnaast zijn er 5 plaatsen voor de meisjesfietsen. Kies nu 1 plaats uit 6 om de jongensfietsen te plaatsen, de overige zijn voor de meisjes (vergelijk [2a])
[2c] na plaatsing van de meisjesfietsen blijven er 6 plaatsen over waar we 3 jongensfietsen en 3 meisjesfietsen moeten plaatsen. (vergelijk [2a])
[2d] aantal meisjesfietsen met een folder is 0,1,2 of 3, de overige folders gaan naar de jongensfietsen (en dat aantal ligt vast).
Re: Telproblemen & kansrekenen (vraag 3)
Op hoeveel manieren kan je 2 ringen uit 5 kiezen?
Op hoeveel manieren kan je 2 ringen uit 4 kiezen?
Op hoeveel manieren kan je 2 ringen uit 3 kiezen?
Hoeveel is dit in totaal?
Op hoeveel manieren kan je 2 ringen uit 4 kiezen?
Op hoeveel manieren kan je 2 ringen uit 3 kiezen?
Hoeveel is dit in totaal?
Re: Telproblemen & kansrekenen (vraag 4 en 5)
Herhalingscombinaties:
[4] op hoeveel manieren kan je 20 identieke voorwerpen over 4 verschillende personen verdelen?
[5] maak een virtueel 5e kleinkind waaraan oma de overgebleven briefjes geeft.
[4] op hoeveel manieren kan je 20 identieke voorwerpen over 4 verschillende personen verdelen?
[5] maak een virtueel 5e kleinkind waaraan oma de overgebleven briefjes geeft.
Re: Telproblemen & kansrekenen (vraag 6)
Aannemende dat dat rooster niet kan roteren (maw: dat duidelijk is wat de bovenkant is):
[6a] 2 mogelijkheden per hokje => voor 16 hokjes .... mogelijkheden
[6b] op hoeveel manieren kan je 8 vakjes uit 16 vakjes kiezen (vergelijk [2a])
[6c] op hoeveel manieren kan je 15 vakjes uit 16 vakjes kiezen, en
op hoeveel manieren kan je 16 vakjes uit 16 vakjes kiezen
Hoeveel mogelijkheden zijn er dus in totaal?
[6a] 2 mogelijkheden per hokje => voor 16 hokjes .... mogelijkheden
[6b] op hoeveel manieren kan je 8 vakjes uit 16 vakjes kiezen (vergelijk [2a])
[6c] op hoeveel manieren kan je 15 vakjes uit 16 vakjes kiezen, en
op hoeveel manieren kan je 16 vakjes uit 16 vakjes kiezen
Hoeveel mogelijkheden zijn er dus in totaal?
Re: Telproblemen & kansrekenen (vraag 7)
[7a en b] je kijkt hier over alle 371 mogelijkheden
[7c]
- gegeven het is maandag, dan zijn er 82 mogelijkheden, hoeveel daarvan in A?
- gegeven het is woensdag, dan zijn er 70 mogelijkheden, hoeveel daarvan in A?
[7c]
- gegeven het is maandag, dan zijn er 82 mogelijkheden, hoeveel daarvan in A?
- gegeven het is woensdag, dan zijn er 70 mogelijkheden, hoeveel daarvan in A?
Re: Telproblemen & kansrekenen (vraag 8)
Er zijn 5C2 * 6C4 = 150 mogelijkheden om de ploeg te vormen (dit zal geen probleem voor je zijn)
[8a] als de vakmanbroer gekozen is, hoeveel mogelijkheden zijn er dan om de overige vakman te kiezen?
als de arbeiderbroer gekozen is, hoeveel mogelijkheden zijn er dan om de overige 3 arbeiders te kiezen?
[8b] op hoeveel manieren kan je 2 vaklui uit 4 kiezen (=de vaklui die niet de broer zijn)
op hoeveel manieren kan je 4 arbeiders uit 5 kiezen (=de arbeiders die niet de broer zijn)
[8a] als de vakmanbroer gekozen is, hoeveel mogelijkheden zijn er dan om de overige vakman te kiezen?
als de arbeiderbroer gekozen is, hoeveel mogelijkheden zijn er dan om de overige 3 arbeiders te kiezen?
[8b] op hoeveel manieren kan je 2 vaklui uit 4 kiezen (=de vaklui die niet de broer zijn)
op hoeveel manieren kan je 4 arbeiders uit 5 kiezen (=de arbeiders die niet de broer zijn)
Re: Telproblemen & kansrekenen (vandaag)
Super super super SUPER hard bedankt! Ik laat vanavond nog iets weten als ik alles opgelost heb!
Re: Telproblemen & kansrekenen (vraag 9 en 10)
[9] Er zijn 6^6 mogelijke uitkomsten: (1,1,1,1,1,1) t/m (6,6,6,6,6,6)
Een goede oplossing is (1,2,3,4,5,6).
Hoeveel permutaties van (1,2,3,4,5,6) bestaan er?
Wat is dus de kans hierop?
[10] nu zijn er 6^7 uitkomsten.
Goede uitkomsten zijn die van opgave [9] met 1 getal extra.
Neem aan dat het extra getal 1 is, dat levert (1,1,2,3,4,5,6).
Hoeveel verschillende rijtjes kan je met deze 7 getallen maken?
Vermenigvuldig dit aantal met 6 (want het extra getal kan ook 2,3,4,5 of 6 zijn) en je hebt het aantal goede uitkomsten.
Wat is dus de kans hierop?
Een goede oplossing is (1,2,3,4,5,6).
Hoeveel permutaties van (1,2,3,4,5,6) bestaan er?
Wat is dus de kans hierop?
[10] nu zijn er 6^7 uitkomsten.
Goede uitkomsten zijn die van opgave [9] met 1 getal extra.
Neem aan dat het extra getal 1 is, dat levert (1,1,2,3,4,5,6).
Hoeveel verschillende rijtjes kan je met deze 7 getallen maken?
Vermenigvuldig dit aantal met 6 (want het extra getal kan ook 2,3,4,5 of 6 zijn) en je hebt het aantal goede uitkomsten.
Wat is dus de kans hierop?
Re: Telproblemen & kansrekenen (vraag 11 en 12)
[11] zal je wel lukken
[12]
Maak een tabel met alle 60 mogelijkheden: voor elke uitkomst van de dobbelsteen zijn er steeds 10 manieren om een bal te trekken:
De kans op elk van deze 60 uitkomsten is even groot.
Hoeveel mogelijkheden zijn er om een witte bal te trekken?
Hoeveel hiervan zijn afkomstig van een 2-ogen-worp?
Hoe groot is dus de gevraagde kans?
[12]
Maak een tabel met alle 60 mogelijkheden: voor elke uitkomst van de dobbelsteen zijn er steeds 10 manieren om een bal te trekken:
Code: Selecteer alles
1: W,W,Z,Z,Z,Z,Z,Z,Z,Z
2: W,W,W,W,Z,Z,Z,Z,Z,Z
3: W,W,Z,Z,Z,Z,Z,Z,Z,Z
4: W,W,W,W,W,Z,Z,Z,Z,Z
5: W,W,Z,Z,Z,Z,Z,Z,Z,Z
6: W,W,W,W,W,Z,Z,Z,Z,ZHoeveel mogelijkheden zijn er om een witte bal te trekken?
Hoeveel hiervan zijn afkomstig van een 2-ogen-worp?
Hoe groot is dus de gevraagde kans?
Re: Telproblemen & kansrekenen (vraag 13)
Binomiale verdeling
[a] p=0.3; (1-p)=q=0.7; n=50; k=25:
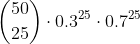
deze heb je waarschijnlijk leren benaderen, klopt dat?
En zo ja: hoe (bv met normale verdeling?) ?
[a] p=0.3; (1-p)=q=0.7; n=50; k=25:
deze heb je waarschijnlijk leren benaderen, klopt dat?
En zo ja: hoe (bv met normale verdeling?) ?
Re: Telproblemen & kansrekenen (vraag 14)
[a] 0.75 * 12
binomiale verdeling, n=12, k=10, p=0.75
[c] binomiale verdeling voor k=10 + k=11 + k=12 (n=12 is wsch te klein om te benaderen)
[d] P(eerste mis) * P(tweede mis) * P(derde raak) = ...
binomiale verdeling, n=12, k=10, p=0.75
[c] binomiale verdeling voor k=10 + k=11 + k=12 (n=12 is wsch te klein om te benaderen)
[d] P(eerste mis) * P(tweede mis) * P(derde raak) = ...
Re: Telproblemen & kansrekenen (vraag 3)
Klopt dit?arie schreef:Op hoeveel manieren kan je 2 ringen uit 5 kiezen?
Op hoeveel manieren kan je 2 ringen uit 4 kiezen?
Op hoeveel manieren kan je 2 ringen uit 3 kiezen?
Hoeveel is dit in totaal?
5 nCr 2 * 4 nCr 2 * 3 nCr 2 = 180

