doorsnede van twee cirkels
-
willemenpjc
- Nieuw lid

- Berichten: 4
- Lid geworden op: 27 mar 2009, 11:06
doorsnede van twee cirkels
De middelpunten van twee cirkels liggen 10 cm van elkaar. Cirkel1 heeft een straal van 8, cirkel2 heeft eenstraal van 5. Hoe kan de oppervlakte van de doorsnede exact berekend worden?
-
horseymanus
- Nieuw lid

- Berichten: 8
- Lid geworden op: 18 mar 2009, 22:01
Re: doorsnede van twee cirkels
Door te integreren
-
willemenpjc
- Nieuw lid

- Berichten: 4
- Lid geworden op: 27 mar 2009, 11:06
Re: doorsnede van twee cirkels
Integreren? Hoe dan?
-
horseymanus
- Nieuw lid

- Berichten: 8
- Lid geworden op: 18 mar 2009, 22:01
Re: doorsnede van twee cirkels
Stel cirkel 1 heeft middelpunt (0,5) en cirkel 2 heeft middelpunt (0, -5)
cirkel 1 voldoet dus aan:
^2 = 64)
Cirkel 2 voldoet aan
^2 = 25)
Snijpunten bevinden zich dan als:

Integreer dus over het interval <-6279/400, 6279/400>
Over de functies:

en

cirkel 1 voldoet dus aan:
Cirkel 2 voldoet aan
Snijpunten bevinden zich dan als:
Integreer dus over het interval <-6279/400, 6279/400>
Over de functies:
en
Re: doorsnede van twee cirkels
Mocht je het onderwerp integratie nog niet gehad hebben: het kan ook zonder:
- kies het middelpunt van cirkel1 (die met straal 8 ) in de oorsprong
- kies het middelpunt van cirkel2 (die met straal 5 ) in punt M = (10, 0)
- noem het snijpunt van de cirkels boven de x-as P en het snijpunt onder de x-as P'
- noem het snijpunt van de lijn PP' met de x-as Q
- noem lengte OQ = x
- hierdoor is lengte QM = 10-x
- noem de lengte van PQ = h
- noem de hoek POQ = alfa
- noem de hoek PMQ = beta
Dan geldt
- volgens Pythagoras: x^2 + h^2 = 8^2 ofwel h^2 = 64 - x^2
- en nogmaals Pythagoras: (10-x)^2 + h^2 = 5^2 ofwel h^2 = 25 - (x-10)^2
Uit beide volgt:
64 - x^2 = 25 - (x-10)^2
bereken hieruit de waarde van x.
Als je x hebt kan je h ook vinden.
Omdat cos(alfa) = x/8 kan je alfa vinden (in graden)
Omdat cos(beta) = (10-x)/5 kan je beta vinden (in graden)
Je weet: de oppervlakte van een cirkel = pi*r^2.
Voor cirkel1 geldt dat de oppervlakte van cirkelsector POP' = ((2*alfa)/360) * pi*8^2
Om de oppervlakte van segment PP' te bereken moet je hier de oppervlakte van
driehoek POP' van aftrekken, deze oppervlakte is h*x.
Voor cirkel2 geldt dat de oppervlakte van cirkelsector PMP' = ((2*beta)/360) * pi*5^2
Om de oppervlakte van segment PP' te bereken moet je hier de oppervlakte van
driehoek PMP' van aftrekken, deze oppervlakte is h*(10-x).
De oppervlakte van de overlap is dan de som van de oppervlakten van deze twee
cirkelsegmenten.
Kom je zo verder??
- kies het middelpunt van cirkel1 (die met straal 8 ) in de oorsprong
- kies het middelpunt van cirkel2 (die met straal 5 ) in punt M = (10, 0)
- noem het snijpunt van de cirkels boven de x-as P en het snijpunt onder de x-as P'
- noem het snijpunt van de lijn PP' met de x-as Q
- noem lengte OQ = x
- hierdoor is lengte QM = 10-x
- noem de lengte van PQ = h
- noem de hoek POQ = alfa
- noem de hoek PMQ = beta
Dan geldt
- volgens Pythagoras: x^2 + h^2 = 8^2 ofwel h^2 = 64 - x^2
- en nogmaals Pythagoras: (10-x)^2 + h^2 = 5^2 ofwel h^2 = 25 - (x-10)^2
Uit beide volgt:
64 - x^2 = 25 - (x-10)^2
bereken hieruit de waarde van x.
Als je x hebt kan je h ook vinden.
Omdat cos(alfa) = x/8 kan je alfa vinden (in graden)
Omdat cos(beta) = (10-x)/5 kan je beta vinden (in graden)
Je weet: de oppervlakte van een cirkel = pi*r^2.
Voor cirkel1 geldt dat de oppervlakte van cirkelsector POP' = ((2*alfa)/360) * pi*8^2
Om de oppervlakte van segment PP' te bereken moet je hier de oppervlakte van
driehoek POP' van aftrekken, deze oppervlakte is h*x.
Voor cirkel2 geldt dat de oppervlakte van cirkelsector PMP' = ((2*beta)/360) * pi*5^2
Om de oppervlakte van segment PP' te bereken moet je hier de oppervlakte van
driehoek PMP' van aftrekken, deze oppervlakte is h*(10-x).
De oppervlakte van de overlap is dan de som van de oppervlakten van deze twee
cirkelsegmenten.
Kom je zo verder??
-
willemenpjc
- Nieuw lid

- Berichten: 4
- Lid geworden op: 27 mar 2009, 11:06
Re: doorsnede van twee cirkels
Bedankt voor je uitgebreide reactie.arie schreef:Mocht je het onderwerp integratie nog niet gehad hebben: het kan ook zonder:
- kies het middelpunt van cirkel1 (die met straal 8 ) in de oorsprong
- kies het middelpunt van cirkel2 (die met straal 5 ) in punt M = (10, 0)
- noem het snijpunt van de cirkels boven de x-as P en het snijpunt onder de x-as P'
- noem het snijpunt van de lijn PP' met de x-as Q
- noem lengte OQ = x
- hierdoor is lengte QM = 10-x
- noem de lengte van PQ = h
- noem de hoek POQ = alfa
- noem de hoek PMQ = beta
Dan geldt
- volgens Pythagoras: x^2 + h^2 = 8^2 ofwel h^2 = 64 - x^2
- en nogmaals Pythagoras: (10-x)^2 + h^2 = 5^2 ofwel h^2 = 25 - (x-10)^2
Uit beide volgt:
64 - x^2 = 25 - (x-10)^2
bereken hieruit de waarde van x.
Als je x hebt kan je h ook vinden.
Omdat cos(alfa) = x/8 kan je alfa vinden (in graden)
Omdat cos(beta) = (10-x)/5 kan je beta vinden (in graden)
Je weet: de oppervlakte van een cirkel = pi*r^2.
Voor cirkel1 geldt dat de oppervlakte van cirkelsector POP' = ((2*alfa)/360) * pi*8^2
Om de oppervlakte van segment PP' te bereken moet je hier de oppervlakte van
driehoek POP' van aftrekken, deze oppervlakte is h*x.
Voor cirkel2 geldt dat de oppervlakte van cirkelsector PMP' = ((2*beta)/360) * pi*5^2
Om de oppervlakte van segment PP' te bereken moet je hier de oppervlakte van
driehoek PMP' van aftrekken, deze oppervlakte is h*(10-x).
De oppervlakte van de overlap is dan de som van de oppervlakten van deze twee
cirkelsegmenten.
Kom je zo verder??
Het is me helemaal duidelijk!
-
willemenpjc
- Nieuw lid

- Berichten: 4
- Lid geworden op: 27 mar 2009, 11:06
Re: doorsnede van twee cirkels
horseymanus schreef:Stel cirkel 1 heeft middelpunt (0,5) en cirkel 2 heeft middelpunt (0, -5)
cirkel 1 voldoet dus aan:
Cirkel 2 voldoet aan
Snijpunten bevinden zich dan als:
Integreer dus over het interval <-6279/400, 6279/400>
Over de functies:
Genoemd interval valt ver buiten mijn geconstruuerde tekening.
Is het wel juist?
Kun je eens voordoen hoe het integreren verder gaat?
en
-
horseymanus
- Nieuw lid

- Berichten: 8
- Lid geworden op: 18 mar 2009, 22:01
Re: doorsnede van twee cirkels
Sorry, ik heb inderdaad een foutje gemaakt.
Het is niet:

maar:

en dus:

De integraal is over de functie

is op te lossen middels een substitutie
)
Daardoor reduceert de integrand tot
)
wat gelijk is aan
 + 1}{2})
Hopelijk is het niet voor het eerste dat je een integraal uitrekent.
Het is niet:
maar:
en dus:
De integraal is over de functie
is op te lossen middels een substitutie
Daardoor reduceert de integrand tot
wat gelijk is aan
Hopelijk is het niet voor het eerste dat je een integraal uitrekent.
Re: doorsnede van twee cirkels
Hmmm
Integreren heeft geen zin jongens!
Met deze formule kan je het algemeen doen.
 en
en  zijn de stralen en
zijn de stralen en  is de afstand tussen de middelpunten.
is de afstand tussen de middelpunten.
Voor als je dit niet wist:) betekent het tegengestelde van
betekent het tegengestelde van ) .
.
m.a.w:) =
=  dus
dus ) =
= 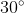
nu nog de formule:
}{180^{\circ}}\cdot\pi\cdot r1^{2}+\frac{cos^{-1}\left(\frac{T^{2}-r1^{2}+r2^{2}}{2\cdot T\cdot r2}\right)}{180^{\circ}}\cdot\pi\cdot r2^{2}- \frac{ \left(T^{2}+r1^{2}-r2^{2}\right) \cdot \sqrt{ r1^{2}- \frac{ \left(T^{2}+r1^{2}-r2^{2}\right)^{2}} {4\cdot T^{2}} } + \left(T^{2}-r1^{2}+r2^{2}\right) \cdot \sqrt{ r2^{2}- \frac{ \left(T^{2}-r1^{2}+r2^{2}\right)^{2}} {4\cdot T^{2}} } } {2\cdot T})
Indien je scherm te klein is, sleep de afbeelding dan naar je URL-balk.
heb ik zelf gevonden op m'n 14 jaar
Bart
Integreren heeft geen zin jongens!
Met deze formule kan je het algemeen doen.
Voor als je dit niet wist:
m.a.w:
nu nog de formule:
Indien je scherm te klein is, sleep de afbeelding dan naar je URL-balk.
heb ik zelf gevonden op m'n 14 jaar
Bart
Laatst gewijzigd door barto op 09 jun 2011, 19:25, 1 keer totaal gewijzigd.
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.
Re: doorsnede van twee cirkels
Als je zo'n lange formule krijgt lijkt voor mij persoonlijk integreren 'interessanter' ...
Re: doorsnede van twee cirkels
Ja misschien wel, maar het klopte ook nog niet helemaal:
zoals ik al zei: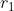 en
en 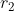 zijn de stralen en
zijn de stralen en  is de afstand tussen de middelpunten.
is de afstand tussen de middelpunten.
Belangrijk: neem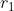 en
en 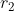 zodat
zodat 
de doorsnede van de 2 cirkels schrijven we wiskundig zo:
\cap c\left(M_2,r_2\right))
Voorwaarden:
(Hoe je iets visueel kan herkennen staat in het groen, en voor als je twijfelt: de wiskundige betekenis staat eronder.)
1: (als de 2 cirkels uit elkaar liggen)
Wiskundig:
\cap c\left(M_2,r_2\right)=0)
2: (als de ene cirkel binnen de andere ligt)
Wiskundig:
\cap c\left(M_2,r_2\right)=\pi*{r_2}^2)
3: (als de cirkels snijpunten hebben)
Wiskundig:
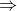 wordt verder opgesplitst:
wordt verder opgesplitst:
Neem twee getallen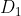 en
en 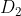 , zodat
, zodat  en
en 
(let op het verschil!)
3a: (het middelpunt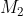 van de kleinste cirkel
van de kleinste cirkel ) ligt buiten de driehoek gevormd door de snijpunten van de cirkels en het middelpunt
ligt buiten de driehoek gevormd door de snijpunten van de cirkels en het middelpunt 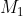 van de grootste cirkel
van de grootste cirkel ) )
)
Wiskundig:
\cap c\left(M_2,r_2\right)=\frac{cos^{-1}\left(\frac{D_1}{r_1}\right)}{180^{\circ}}*\pi*{r_1}^2-\sqrt{{r1}^2-{D_1}^2}*D_1+\frac{cos^{-1}\left(\frac{D_2}{r_2}\right)}{180^{\circ}}*\pi*{r_2}^2-\sqrt{{r_2}^2-{D_2}^2}*D_2)
(sleep de afbeelding naar je URL-balk als je scherm te klein is)
Hierbij is het belangrijk dat je de positieve) neemt!
neemt!
Ik had al gezegd dat=\frac{\sqrt{3}}{3})
en dat=30^{\circ})
maar niet dat=-30^{\circ})
Die positieve moet je hebben.
3b: (de snijpunten van de cirkels en het middelpunt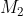 van de kleinste cirkel
van de kleinste cirkel ) zijn colineair)
zijn colineair)
Wiskundig: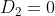
\cap c\left(M_2,r_2\right)=\frac{\pi*{r_2}^2}{2}+\frac{cos^{-1}\left(\frac{T}{r_1}\right)}{180^{\circ}}*\pi*{r_1}^2-T*r_2)
3c: (het middelpunt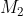 van de kleinste cirkel
van de kleinste cirkel ) ligt binnen de driehoek gevormd door de snijpunten van de cirkels en het middelpunt
ligt binnen de driehoek gevormd door de snijpunten van de cirkels en het middelpunt 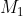 van de grootste cirkel
van de grootste cirkel ) )
)
Wiskundig:
\cap c\left(M_2,r_2\right)=\left[1-\frac{cos^{-1}\left(\frac{D_1}{r_1}\right)}{180^{\circ}}\right]*\pi*{r_2}^2+\left(\sqrt{{r_2}^2-{D_1}^2}-\sqrt{{r_1}^2-{D_1}^2}\right)*D_1+\frac{cos^{-1}\left(\frac{D_1}{r_1}\right)}{180^{\circ}}*\pi*{r_1}^2)
(sleep de afbeelding naar je URL-balk als je scherm te klein is)
Ik zou het bewijs hier wel bij willen zetten, maar dan wordt dit antwoord nog 10 keer zo lang
zoals ik al zei:
Belangrijk: neem
de doorsnede van de 2 cirkels schrijven we wiskundig zo:
Voorwaarden:
(Hoe je iets visueel kan herkennen staat in het groen, en voor als je twijfelt: de wiskundige betekenis staat eronder.)
1: (als de 2 cirkels uit elkaar liggen)
Wiskundig:
2: (als de ene cirkel binnen de andere ligt)
Wiskundig:
3: (als de cirkels snijpunten hebben)
Wiskundig:
Neem twee getallen
(let op het verschil!)
3a: (het middelpunt
Wiskundig:
(sleep de afbeelding naar je URL-balk als je scherm te klein is)
Hierbij is het belangrijk dat je de positieve
Ik had al gezegd dat
en dat
maar niet dat
Die positieve moet je hebben.
3b: (de snijpunten van de cirkels en het middelpunt
Wiskundig:
3c: (het middelpunt
Wiskundig:
(sleep de afbeelding naar je URL-balk als je scherm te klein is)
Ik zou het bewijs hier wel bij willen zetten, maar dan wordt dit antwoord nog 10 keer zo lang
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.
Re: doorsnede van twee cirkels
Hoi, ik was even op zoek naar de oplossing voor de oppervlakte van de doorsnede van 2 cirkels en kwam hier terecht.
De reden waarom ik me eigenlijk geregistreerd heb, wat ik eigenlijk normaal nooit doe, is om het volgende aan te duiden:
Cos(30°) = vk(3)/2
 doei doei
doei doei
De reden waarom ik me eigenlijk geregistreerd heb, wat ik eigenlijk normaal nooit doe, is om het volgende aan te duiden:
Cos(30°) = vk(3)/2
Re: doorsnede van twee cirkels
Wat is de vraag, waar je dit kan vinden (er is nl een lijstje) of waarom dat zo is?Carrein schreef: Cos(30°) = vk(3)/2
Re: doorsnede van twee cirkels
Het was de oplossing van Barto die vermeldde dat cos30° gelijk was aan vk(3)/3, terwijl dat niet zo is.
Er is een bekende lijst met vierkantswortels ter vermakkelijking van berekenen (zonder dat je je rekenmachine erbij hoeft te halen en problemen krijgt met afrondingsfouten)
Wel kan ik momenteel geen vertrouwelijke bron geven, maar je moet m'n woord ervoor maar nemen
http://nl.wikipedia.org/wiki/Sinus_en_cosinus
Er is een bekende lijst met vierkantswortels ter vermakkelijking van berekenen (zonder dat je je rekenmachine erbij hoeft te halen en problemen krijgt met afrondingsfouten)
Wel kan ik momenteel geen vertrouwelijke bron geven, maar je moet m'n woord ervoor maar nemen
http://nl.wikipedia.org/wiki/Sinus_en_cosinus
Re: doorsnede van twee cirkels
inderdaad, klein foutje 
maar mijn formules kloppen nog steeds
maar mijn formules kloppen nog steeds
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.


