Plezante vergelijking
Re: Plezante vergelijking
Dat levert



Re: Plezante vergelijking
Helemaal correct!
Euhm, ik bedoelde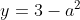 , bijvoorbeeld.
, bijvoorbeeld.
Euhm, ik bedoelde
Veel (relevante) dingen zijn er niet om in te vullen op de puntjes.SafeX schreef:Noem je dit een aanwijzing of een uitdaging?
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.
Re: Plezante vergelijking
en nu???
Re: Plezante vergelijking
Wel, \cdot(...)) .
.
(Waarom die kwadratische vergelijking, dit is bedoeld om een mooie oplossing te zijn, weet je nog? )
)
(Waarom die kwadratische vergelijking, dit is bedoeld om een mooie oplossing te zijn, weet je nog?
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.
Re: Plezante vergelijking
Leuk vraagstukje !
Ik heb de subtituties gegeven door Barto overgenomen : y = x/6! -> 1
a^2 = 3-y -> y = 3-a^2 -> 2
b^2 = 4-y -> b^2 = a^2 + 1 -> 3
c^2 = 5-y -> c^2 = a^2 + 2 -> 4
De vgl. wordt nu : y=a.b+b.c+a.c -> y-b.c = a.(b+c) -> 5
Kwadrateren van beide leden en invullen van b^2 en C^2 uit (3) en (4) geeft :
y^2 -2.b.c.(y+a^2)= a^4 -2 -> 6
Invullen van y uit (2)in (6)geeft : 6.b.c = 11-6.a^2 -> 7
Invullen van b en c uit (3)en (4) in (7)en daarna kwadrateren.
Dit geeft : a^2=49/240 -> 8
Nu is y = 3-a^2 = 671/240 = x/720 (-> de y-waarde uit (1)= de y-waarde uit (2))
Oplossing : x = 720.671/240 --> x = 2013 -> 9
Ik heb de subtituties gegeven door Barto overgenomen : y = x/6! -> 1
a^2 = 3-y -> y = 3-a^2 -> 2
b^2 = 4-y -> b^2 = a^2 + 1 -> 3
c^2 = 5-y -> c^2 = a^2 + 2 -> 4
De vgl. wordt nu : y=a.b+b.c+a.c -> y-b.c = a.(b+c) -> 5
Kwadrateren van beide leden en invullen van b^2 en C^2 uit (3) en (4) geeft :
y^2 -2.b.c.(y+a^2)= a^4 -2 -> 6
Invullen van y uit (2)in (6)geeft : 6.b.c = 11-6.a^2 -> 7
Invullen van b en c uit (3)en (4) in (7)en daarna kwadrateren.
Dit geeft : a^2=49/240 -> 8
Nu is y = 3-a^2 = 671/240 = x/720 (-> de y-waarde uit (1)= de y-waarde uit (2))
Oplossing : x = 720.671/240 --> x = 2013 -> 9
Re: Plezante vergelijking
Zo gaat het inderdaad, maar waar ik naartoe wou is (a+c)) ,
, (b+c)) en
en (b+c)) . Dit kan makkelijk opgelost worden naar a.
. Dit kan makkelijk opgelost worden naar a.
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.




