machtsverheffingen van x
machtsverheffingen van x
Hier nog een aardig vraagje. Let wel met het juiste trucje is de oplossing erg gemakkelijk !
Bepaal de waarde van X in de volgende vergelijking:
x^{x^{x^{x^{x^{x}}}}}=2
Hierbij staat dus X tot de macht X, en nog eens tot de macht X, en nog eens tot de macht X enz...
Deze machtsverheffing gaat oneindig lang door ! Het geheel is gelijk aan 2.
Hoeveel is X dan ?
Bepaal de waarde van X in de volgende vergelijking:
x^{x^{x^{x^{x^{x}}}}}=2
Hierbij staat dus X tot de macht X, en nog eens tot de macht X, en nog eens tot de macht X enz...
Deze machtsverheffing gaat oneindig lang door ! Het geheel is gelijk aan 2.
Hoeveel is X dan ?
Re: machtsverheffingen van x
De meest lastige vraag hier vind ik is
Hoe zou je x^{x^{x^{x^{x^{x...}}}}} omschrijven in woorden?
Ik zou
^{x})^{...}}}}) , wat niet is wat je wilt.
, wat niet is wat je wilt.
Maar je hebt:
[ formule]u_0 = x[/formule]
[ formule]u_n = x^{u_{n-1}}[/formule] voor positieve gehele n.
Met [ formule]\lim_{n \to \infty} u_n = 2[/formule]
Nu geldt ook [ formule]\lim_{n \to \infty} u_n = \lim_{n \to \infty} u_{n-1}[/formule] ofwel 2 = x^2 zodat x = sqrt(2).
Hoe zou je x^{x^{x^{x^{x^{x...}}}}} omschrijven in woorden?
Ik zou
lezen alsparref schreef:X tot de macht X, en nog eens tot de macht X, en nog eens tot de macht X enz...
Maar je hebt:
[ formule]u_0 = x[/formule]
[ formule]u_n = x^{u_{n-1}}[/formule] voor positieve gehele n.
Met [ formule]\lim_{n \to \infty} u_n = 2[/formule]
Nu geldt ook [ formule]\lim_{n \to \infty} u_n = \lim_{n \to \infty} u_{n-1}[/formule] ofwel 2 = x^2 zodat x = sqrt(2).
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: machtsverheffingen van x
Indien U alle haakjes weglaat in Uw formule dan bent U goed!
(Sorry, maar ik ben nog niet zo goed thuis in deze editor want ik nieuw. Ik had geprobeerd om dit weer te geven via copie/paste vanuit een ander programma maar dit is niet gelukt.)
(Sorry, maar ik ben nog niet zo goed thuis in deze editor want ik nieuw. Ik had geprobeerd om dit weer te geven via copie/paste vanuit een ander programma maar dit is niet gelukt.)
Re: machtsverheffingen van x
Beste David,
De bedoeling is x tot de macht x en nog eens tot de macht x en nog eens tot de macht x enz.. en dit een oneindig aantal malen. Dus geen haakjes gebruiken !
Uw gegeven formule is ok !, mits U de haakjes weglaat.
Deze correcte weergave lukt mij niet met deze editor. Wellicht lukt het U wel.
Bedankt !
De bedoeling is x tot de macht x en nog eens tot de macht x en nog eens tot de macht x enz.. en dit een oneindig aantal malen. Dus geen haakjes gebruiken !
Uw gegeven formule is ok !, mits U de haakjes weglaat.
Deze correcte weergave lukt mij niet met deze editor. Wellicht lukt het U wel.
Bedankt !
Re: machtsverheffingen van x
Je LaTeX is goed! Hieronder staat het met de tags eromheen. Je kan kopiëren uit de code. Ik had mijn oplossing onderaan mijn vorige post gezet, alleen kan je het niet zien. Het is in LaTeX-code, maar de tags heb ik bewerkt dus er wordt geen LaTeX getoond.
Gebruik
voor
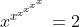
Of
voor
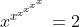
Gebruik
Code: Selecteer alles
[formule]x^{x^{x^{x^{x^{x}}}}}=2[/formule]Of
Code: Selecteer alles
[tex]x^{x^{x^{x^{x^{x}}}}}=2[/tex]Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: machtsverheffingen van x
De oplossing vinden, als gegeven is dat er een oplossing IS, is niet erg lastig. Het kan ook leuk zijn om aan te tonen dat de 'power-tower' inderdaad convergeert.
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.
Re: machtsverheffingen van x
Volgens mijn truc zou de uitkomst moeten zijn
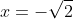
Klopt dat?
Vind je mijn truc overtuigend?
Klopt dat?
Vind je mijn truc overtuigend?
Re: machtsverheffingen van x
Hm, alleen ) ? parref vraagt voor een waarde voor x (laten we het maar bij de kleine letter houden). Maar misschien is er meer dan een x.
? parref vraagt voor een waarde voor x (laten we het maar bij de kleine letter houden). Maar misschien is er meer dan een x.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: machtsverheffingen van x
Misschien zijn er wel géén oplossingen.
Geloof je dat mijn oplossing een echte oplossing is?
Ik ben daar niet zo zeker van.
Zonder convergentiebewijs overtuigt me geen enkele truc.
Geloof je dat mijn oplossing een echte oplossing is?
Ik ben daar niet zo zeker van.
Zonder convergentiebewijs overtuigt me geen enkele truc.
Re: machtsverheffingen van x
Kan zijn, ik geloof dat sqrt(2) wel een oplossing is. x^(x^2) = 2 geeft ook x=-sqrt(2). Ik had de functie zo bekeken.op=op schreef:Misschien zijn er wel géén oplossingen.
Wat 2 nadert als n toeneemt.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: machtsverheffingen van x
Welk argument heb je daar voor? Stijgend en begrensd?David schreef: Wat 2 nadert als n toeneemt.
Re: machtsverheffingen van x
Los op
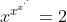 .
.
Wat denk je van de volgende redenering:
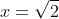 kan geen oplossing zijn, want dan komt er 4 uit
kan geen oplossing zijn, want dan komt er 4 uit
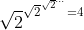
Ga maar na met je truc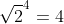 .
.
Wat denk je van de volgende redenering:
Ga maar na met je truc
Re: machtsverheffingen van x
op=op schreef:Los op
.
Wat denk je van de volgende redenering:
kan geen oplossing zijn, want dan komt er 4 uit
Ga maar na met je truc.
Wat met de volgende 'redenering': het is 5 omdat het 5 is...
De veronderstelling
Met inductie heb jeop=op schreef:Welk argument heb je daar voor? Stijgend en begrensd?David schreef: Wat 2 nadert als n toeneemt.
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.
Re: machtsverheffingen van x
komt niet uit de lucht vallen. Het is jouw truc die uit de lucht komt vallen.
Om
Dan is
Nu jij met jouw 5.
Dit is de essentie van het probleem.
Re: machtsverheffingen van x
Allen bedankt voor Uw reacties.. De ene benadert het al beter dan de andere..
De bedoeling is dan iedereen het moet kunnen en dus ook diegene die geen rekenmachine hebben..
Ik ga 2 hints geven :
1- De waarde x is begrensd tussen : 1 < x < 2
want bij x = 1 blijft de waarde onder de torenpower gelijk aan 1
en voor x = 2 gaan we na enkele machtsverheffingen al zeer snel zeer grote waardes bekomen !
2- Wat gebeurt er indien we onder de powertoren nog een x plaatsen ? Verandert de waarde van de
powertoren daardoor ?
Voor de elektronici onder jullie : wat doen we als we b.v. de ingangsimpedantie moeten bepalen
van een keten waarbij een oneindig aantal gelijke deelcircuitjes na elkaar geplaatst worden ?
Noot: In plaats van = 2 kunnen we de powertoren ook gelijkstellen aan een willekeurig getal n,
lopend vanaf 0 tot oneindig. In al deze gevallen is de uitkomst begrensd. Hierop kom ik
later op terug..
De bedoeling is dan iedereen het moet kunnen en dus ook diegene die geen rekenmachine hebben..
Ik ga 2 hints geven :
1- De waarde x is begrensd tussen : 1 < x < 2
want bij x = 1 blijft de waarde onder de torenpower gelijk aan 1
en voor x = 2 gaan we na enkele machtsverheffingen al zeer snel zeer grote waardes bekomen !
2- Wat gebeurt er indien we onder de powertoren nog een x plaatsen ? Verandert de waarde van de
powertoren daardoor ?
Voor de elektronici onder jullie : wat doen we als we b.v. de ingangsimpedantie moeten bepalen
van een keten waarbij een oneindig aantal gelijke deelcircuitjes na elkaar geplaatst worden ?
Noot: In plaats van = 2 kunnen we de powertoren ook gelijkstellen aan een willekeurig getal n,
lopend vanaf 0 tot oneindig. In al deze gevallen is de uitkomst begrensd. Hierop kom ik
later op terug..




