gekleurde ballen [20+]
gekleurde ballen [20+]
Een doos bevat n gekleurde ballen die elk een verschillende kleur hebben. Je neemt telkens 2 gekleurde ballen en verandert de kleur van de tweede bal in de kleur van de eerste bal. Hoeveel keer moet je gemiddeld dit proces herhalen eer alle ballen dezelfde kleur hebben?
Re: gekleurde ballen [20+]
+20 ballenwnvl schreef:Een doos bevat n gekleurde ballen die elk een verschillende kleur hebben. Je neemt telkens 2 gekleurde ballen en verandert de kleur van de tweede bal in de kleur van de eerste bal. Hoeveel keer moet je gemiddeld dit proces herhalen eer alle ballen dezelfde kleur hebben?
bij 24 ballen = 12 kleuren na 1 keer
24 ballen 12 kleuren
optimaal blijven er 6 kleuren over
in slechtste geval blijven er 12 kleuren over
6+12 = 18 , 18/2 = 9
hieruit kan je afleiden dat het steeds 3/4 kleuren gemiddeld overblijven
aangezien het gemiddeld is moet je niet afronden naar volledige getallen.
24 → 12 , 9 , 6,75 , 5,0625 , 3,796875 , 2,84765625 , 2,1357421875 , 1,601806640625 , 1,20135498046875 , 0,90.... = 10 keer bij 24 ballen, bij 32 ballen 11 keer enz....
Re: gekleurde ballen [20+]
Mogelijk is de vraag verkeerd begrepen. Na 1 keer zou je vertrekkend van 24 kleuren. 23 kleuren hebben. Van 1 kleur zou je 2 ballen hebben.
Re: gekleurde ballen [20+]
Een eerste aanzet.
Ik ga uit van een van de kleuren, zeg wit.
Alle kleuren die niet wit zijn noem ik zwart. (zwart = niet-wit)
Het "spel" kan eindigen (als het al ooit eindigt) in alles wit of alles zwart (=alle witten foetsie).
E(k) is verwachte aantal zetten om k witten te krijgen.
E(k+1) = E(k).k(n-k)/n² + E(k+2).(k+2)(n-k-2)/n²
randvoorwaarden daargelaten.
E(0) en E(n) zouden hieruit berekend kunnen worden.
Het wordt nu iets te heet in de kamer en dus ook in mijn bovenkamer, dus tot zover.
Ik ga uit van een van de kleuren, zeg wit.
Alle kleuren die niet wit zijn noem ik zwart. (zwart = niet-wit)
Het "spel" kan eindigen (als het al ooit eindigt) in alles wit of alles zwart (=alle witten foetsie).
E(k) is verwachte aantal zetten om k witten te krijgen.
E(k+1) = E(k).k(n-k)/n² + E(k+2).(k+2)(n-k-2)/n²
randvoorwaarden daargelaten.
E(0) en E(n) zouden hieruit berekend kunnen worden.
Het wordt nu iets te heet in de kamer en dus ook in mijn bovenkamer, dus tot zover.
Re: gekleurde ballen [20+]
Met simulatie: (n - 1)^2? De resultaten liggen er erg dichtbij.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: gekleurde ballen [20+]
Ik denk dat het te bewijzen is met een Markovketen dat het proces ooit eindigt.[b][color=#8400BD]op=op[/color][/b] schreef:...(als het al ooit eindigt)...
De toestanden zijn de partities van n.
Dus als n = 5 zijn de toestanden:
5, 1 + 4, 2 + 3, 1 + 1 + 3, 1 + 2 + 2, 1 + 1 + 1 + 2, 1 + 1 + 1 + 1 + 1. (7 toestanden).
Elke term stelt een andere kleur voor. De waarde van de term zegt hoe vaak een kleur voorkomt.
Een 'stap' die wnvl hierboven beschreef is hier als volgt:
Kies twee verschillende termen (onthoud volgorde). Trek van de eerste term 1 af. Tel bij de tweede term 1 op. Als de eerste term nul is, neem het niet mee in de som.
Op deze manier kan een transitiematrix worden opgesteld met op de diagonaal een 1 (voor partitie 'n'). Daarmee is bewezen dat het proces eindigt.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: gekleurde ballen [20+]
Die opgave dateert al van bijna 3 jaar geleden en intussen ben ik zelf vergeten wat de oplossingsstrategie was. Ik herinner me wel dat er een hele mooie oplossing was. Ik zoek zelf ook terug verder.
Het was een licht aangepaste variant op een bestaand probleem uit de literatuur. Ik was er opgekomen in het kader van een poging om een Project Euler probleem te verzinnen.
Het was een licht aangepaste variant op een bestaand probleem uit de literatuur. Ik was er opgekomen in het kader van een poging om een Project Euler probleem te verzinnen.
Re: gekleurde ballen [20+]
Het proces hoeft niet te eindigen, het verwacht aantal trekkingen zal wel eindig zijn.David schreef:Ik denk dat het te bewijzen is met een Markovketen dat het proces ooit eindigt.[b][color=#8400BD]op=op[/color][/b] schreef:...(als het al ooit eindigt)...
Het is inderdaad een Markov proces, Maar alle toestanden uitwerken is niet doenbaar.
Laatst gewijzigd door wnvl op 05 jul 2015, 23:51, 1 keer totaal gewijzigd.
Re: gekleurde ballen [20+]
Zou heel goed kunnen dat dit juist is. De oplossing was relatief eenvoudig.David schreef:Met simulatie: (n - 1)^2? De resultaten liggen er erg dichtbij.
Re: gekleurde ballen [20+]
Het is ook een mooi probleem![color=#8400BD][b]wnvl[/b][/color] schreef:Ik herinner me wel dat er een hele mooie oplossing was.
De kans dat het niet eindigt is 0, dus we kunnen toch zeggen dat het eindigt? Het is als de vraag:[color=#8400BD][b]wnvl[/b][/color] schreef:Het proces hoeft niet te eindigen...
(Veronderstel onbeperkt leven, energie en doorzettingsvermogen etc.) Gooi een dobbelsteen tot je 6 gooit. Stop je ooit? Ik denk 'ja'.
Er zijn evenveel toestanden als partities van n, waarvan een tabel hier staat.[color=#8400BD][b]wnvl[/b][/color] schreef:...Maar alle toestanden uitwerken is niet doenbaar.
Stel R(n) is het verwachte aantal stappen uit de oplossing. Is het misschien op te lossen door te kijken naar n kleuren waarvan een kleur twee keer voorkomt? Die toestand is na een stap vanaf n + 1 verschillende kleurende ballen die elk een keer voorkomen.[color=#8400BD][b]wnvl[/b][/color] schreef:De oplossing was relatief eenvoudig.
Heb je hier (na die tijd) nog links voor?[color=#8400BD][b]wnvl[/b][/color] schreef:Het was een licht aangepaste variant op een bestaand probleem uit de literatuur. Ik was er opgekomen in het kader van een poging om een Project Euler probleem te verzinnen.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: gekleurde ballen [20+]
Zonder onderzoek naar de praktijk, kan dit probleem worden gesplitst in het verwachte aantal stappen om een kleur kwijt te raken. Dit geeft n - 1 transitiematrices met stadia partities van k en k + 1 met 1 <= k <= n-1, maar veel minder velden per matrix en in het totaal. (Zie rij http://oeis.org/A008284)Ik schreef: Er zijn evenveel toestanden als partities van n, waarvan een tabel hier staat.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: gekleurde ballen [20+]
Met partities werken wordt veel te ingewikkeld. Wat me wel bekoort is na te gaan in hoeveel stappen een kleur verdwijnt.David schreef:
Zonder onderzoek naar de praktijk, kan dit probleem worden gesplitst in het verwachte aantal stappen om een kleur kwijt te raken.
Laten we zeggen kleur wit.
Het doet er dan niet toe hoe de anderen gekleurd zijn. Je hoeft je allleen maar te concentreren op het aantal witten.
Dit lijkt me uit te rekenen.
De vraagt die dan volgt is, wat is het aantal stappen opdat 2 kleuren verdwijnen.
In dat geval mogen de twee kleuren 1 naam geven, zeg wit en de overigen afdoen met kleur zwart.
enz.
Re: gekleurde ballen [20+]
Waarschijnlijk wel, maar ik zie even geen andere manier (en het geeft me wat oefening).[color=#8400BD][b]op=op[/b][/color] schreef:Met partities werken wordt veel te ingewikkeld.
Reductie naar twee kleuren kan een mooie vereenvoudiging zijn, maar hoe zit het als wit niet verdwijnt maar als laatst overblijft? Het lijkt me dat als je een kleur kiest waar je bijhoudt hoe lang het duurt voor die verdwijnt, je een ander resultaat krijgt dan als je wacht tot er een willekeurige kleur verdwijnt.[color=#8400BD][b]op=op[/b][/color] schreef:Het doet er dan niet toe hoe de anderen gekleurd zijn.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: gekleurde ballen [20+]
Weer een simulatie gedraaid, dit keer om te bepalen hoeveel stappen het duurt om met n ballen van k naar k - 1 verschillende kleuren te gaan. Het lijkt erop dat dat naar verwachting gebeurt in 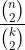 stappen met 2 <= k <= n.
stappen met 2 <= k <= n.
Hieronder is de code, voor PARI/gp: http://pari.math.u-bordeaux.fr/, voor wie wil herproduceren/inspecteren o.i.d.
(mainstep(3) duurde ongeveer 3 seconden, mainstep(20) ongeveer 70 minuten.)
Hieronder is de code, voor PARI/gp: http://pari.math.u-bordeaux.fr/, voor wie wil herproduceren/inspecteren o.i.d.
Code: Selecteer alles
addhelp(mainstep, "Matrix met in de m-de rij 'gemstep' voor m + 1 ballen.")
mainstep(n) = {
m=matrix(n-1,n-1);
for(i=2,n,
r=gemstep(i,1e5);for(j=1,#r,m[i-1,j]=r[j])
);m
}
addhelp(gemstep, "Voor n elementen. Het 1e element geeft het gemiddeld aantal stappen om de eerste kleur te verliezen, het tweede element (if there) de tweede kleur etc.")
gemstep(n,{q=10000}) = 1.*sum(i=1,q,boxstep(n))/q
addhelp(boxstep,"box met n verschillende kleuren. Resultaat: vector met aantal stappen om een 1..n-1 kleuren te verliezen")
boxstep(n) = {my(v=vector(n,i,i),t,r=vector(n-1),q=n);
while(#Set(v)>1,
v = iteratie(v);t++;
if(#Set(v)<q,r[n+1-q]=t;t=0;q--)
);r
}
addhelp(iteratie,"uit de 'bak met ballen', pak twee (verschillende!) ballen, en geef het eerste de kleur van het tweede.")
iteratie(v) = {
my(i1 = random(#v)+1,
i2 = random(#v)+1);
while(i1==i2,
i2=random(#v)+1;
);
v[i1]=v[i2];v
}
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: gekleurde ballen [20+]
Bovenstaande is equivalent met:
^2)
(voor n > 0).
Het bewijs van gelijkheid is denk ik tweeledig. We kunnen buiten de som halen, en kijken wat
buiten de som halen, en kijken wat 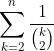 geeft.
geeft.
Inspectie doet vermoeden: .
.
Met inductie:
Voor n = 1 hebben we in het linkerlid de lege som, ofwel 0. Rechts hebben we (2 * 1 - 2)/1 = 0. Dus waar voor n = 1.
} + \frac{2n - 2}{n} = \frac{2}{n(n+1)} + \frac{(2n - 2)(n+1)}{n(n+1)} \\\\ = \frac{2}{n(n+1)} + \frac{(2n - 2)(n+1)}{n(n+1)} \\\\ = \frac{2n^2 - 2n + 2n - 2 + 2}{n(n+1)} \\\\ = \frac{2n}{n + 1} = \frac{2(n + 1) - 2}{n+1})
Dat voor het eerste deel.
Nu,}{2} \cdot \frac{2n-2}{n} = (n-1)^2) .
.
Dat was te bewijzen.
De gevonden resultaten spreken elkaar in ieder geval niet tegen.
(voor n > 0).
Het bewijs van gelijkheid is denk ik tweeledig. We kunnen
Inspectie doet vermoeden:
Met inductie:
Voor n = 1 hebben we in het linkerlid de lege som, ofwel 0. Rechts hebben we (2 * 1 - 2)/1 = 0. Dus waar voor n = 1.
Dat voor het eerste deel.
Nu,
Dat was te bewijzen.
De gevonden resultaten spreken elkaar in ieder geval niet tegen.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)




