We zijn op zoek naar b waarvoor:
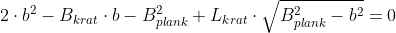
of anders gezegd: de b waarvoor deze functie de waarde nul oplevert:
 \;=\; 2\cdot b^2 - B_{krat}\cdot b - B_{plank}^2 + L_{krat}\cdot \sqrt{B_{plank}^2-b^2})
Uit bovenstaande figuur weten we dat b groter moet zijn dan nul, en kleiner dan B_plank.
We kunnen nu de halveringsmethode (
https://nl.wikipedia.org/wiki/Halveringsmethode)
gebruiken om onze b te vinden.
In Excel komt dit er zo uit te zien (de cursor staat op cel C6):

Regel 1 t/m 5 zijn tekst.
De constanten waar we mee werken staan in B1, B2 en B3
b ligt tussen 0 en Bplank, daar starten we mee:
cel B6 => 0
cel F6 => =$B$3
dan bepalen we het midden van (de huidige) bmin en bmax:
cel D6 => =(B6+F6)/2
Bereken dan de waarden die de functie f() aanneemt voor bmin, bmid en bmax:
cel C6 => =2*B6^2 -$B$2*B6 -$B$3^2 + $B$1*SQRT($B$3^2-B6^2)
cel E6 => =2*D6^2 -$B$2*D6 -$B$3^2 + $B$1*SQRT($B$3^2-D6^2)
cel G6 => =2*F6^2 -$B$2*F6 -$B$3^2 + $B$1*SQRT($B$3^2-F6^2)
(als je een Nederlanse versie hebt is SQRT waarschijnlijk WORTEL)
In regel 6 zien we dan:
f(0) = 40000
f(50) = 23301.27
f(100) = -20000
Nu passen we de halveringsmethode toe:
f(0) is positief, f(100) is negatief.
f(50) is positief, dus de waarde van b waarvoor f(b) nul is, zal liggen tussen 50 en 100:
50 < b < 100
In de volgende stap nemen we daarom bmin=50 en bmax=100.
In Excel vertaalt deze methode naar:
cel B7 => =IF(E6>0;D6;B6)
cel F7 => =IF(E6<=0;D6;F6)
(in Nederlands: =ALS(E6<=0;D6;F6), afhankelijk van je instellingen kan ; ook , zijn)
Copy/paste de cellen C6, D6, E6 en G6 naar resp. C7, D7, E7 en G7
En deze halveringen gaan we nu een aantal keren herhalen:
Copy/paste de hele regel 7 naar regel 8 t/m 28
Elke herhaling levert een halvering van het interval [bmin, bmax],
10 herhalingen geven dan ongeveer 3 significante cijfers
20 herhalingen 6 significante cijfers.
(indien nodig kan je nog veel meer herhalingen toevoegen).
Tenslotte voeren we de eindberekening uit:
cel B30 => =D28
cel B31 => =SQRT($B$3^2-B30^2)
cel B32 => =$B$3*($B$1-B31)/B30
met in kolom A de betekenis van deze getallen.




