Pagina 1 van 1
Parabool opstellen
Geplaatst: 10 nov 2018, 13:44
door Black9
Hallo allen,
Ik ben bezig met een parabool op te stellen maar ik kom er niet uit.
Het is een dyno chart voor een auto.
De grafiek snijdt in twee punten. (0:0) en (8000:1000) en het top punt is (6000:1371)
Kan iemand me helpen?
Re: Parabool opstellen
Geplaatst: 10 nov 2018, 14:07
door SafeX
Wat heb je al geprobeerd?
De gezochte parabool is van de vorm: f(x)=a(x-p)^2+q
Kan je dat verklaren? Wat is (bv) de betekenis van het punt (p,q) van de parabool?
Re: Parabool opstellen
Geplaatst: 10 nov 2018, 14:19
door Black9
Ik had al iets van
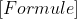
y=-sqrt(0.0000000014503402777)(x-6000)^2+1371
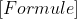
alleen dan gaat hij nog niet door het punt (8000:1000)
Re: Parabool opstellen
Geplaatst: 10 nov 2018, 18:01
door arno
Ik had al iets van
(x-6000)^2+1371)
alleen dan gaat hij nog niet door het punt (8000:1000)
Kun je eens aangeven waar je de getallen die jij noemt vandaan hebt? Ben je bekend met het opstellen van de vergelijking van een parabool aan de hand van de coördinaten van de top van de parabool?
Re: Parabool opstellen
Geplaatst: 10 nov 2018, 19:43
door SafeX
Black9 schreef: ↑10 nov 2018, 14:19
^2+1371
)
De functie klopt behalve het getal (de wortel van). Hoe kom je daaraan?
Je kan, naast het toppunt, slechts één van beide andere punten gebruiken. Maw de gevraagde parabool kan niet door al die gegeven punten gaan en aan de eis van het toppunt voldoen.
Re: Parabool opstellen
Geplaatst: 10 nov 2018, 23:37
door Black9
Ik had dit getal gevonden door wat in een parabool calculator te frutselen.
ik kwam eerst op een getal dat eindigde met alleen maar 3en. en door het te kwadrateren werd het een 'mooi' getal. En met dit getal gaat de formule dus door (0:0). Vandaar dit getal.
Ik dacht dat er ook nog parabolen 'bestonden' die soort van schuin liepen. Dus dat ze eerst om hoog gaan tot een top punt en daarna weer steiler kunnen dalen. Maar aangezien ik dat niet wist kwam ik hier terecht.
Re: Parabool opstellen
Geplaatst: 11 nov 2018, 10:40
door arie

Er zijn genoeg curves te bedenken die aan je vier voorwaarden voldoen,
bijvoorbeeld deze hyperbool:
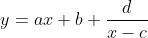
met in dit geval:
a = 0.516911585...
b = 2184.1901769...
c = 13573.1707317...
d = 29646386.1826...
Voor praktijkproblemen (zoals je dyno chart) zoek je echter bij voorkeur een formule die overeenkomt met de theoretische achtergrond van je probleem.
Heb je wellicht een algemene formule waar dyno charts aan voldoen?
Zo niet, dan zou je ook nog kunnen overwegen om statistische methoden te gebruiken om de best passende curve door een aantal punten te vinden. En dan geldt in het algemeen: hoe meer punten van de grafiek bekend zijn, hoe beter het resultaat.
Re: Parabool opstellen
Geplaatst: 11 nov 2018, 19:08
door Black9
Dankjewel arie,
dit was exact wat ik zocht!
Het was inderdaad geen parabool maar een hyperbool.
