Bepalen van beeld van een lineaire afbeelding
Bepalen van beeld van een lineaire afbeelding
Gegeven is volgende lineaire afbeelding:
f: R3[X] --> R4[X]
f(P(X)) = x² P'(X) + x P''(X) + P'''(X) + (x^4 + x² +2)P'(0)
Hoe bepaal je het beeld van deze afbeelding? Ik heb al een basis voor de kern: B=(1), dus dat betekent dat het beeld dimensie 3 moet hebben. Heeft het iets te maken met het feit dat je de vierdemachtsterm in functie van de tweedemachtsterm kunt schrijven (en hetzelf voor de derde en de eerste machtsterm) ?
Thanks
f: R3[X] --> R4[X]
f(P(X)) = x² P'(X) + x P''(X) + P'''(X) + (x^4 + x² +2)P'(0)
Hoe bepaal je het beeld van deze afbeelding? Ik heb al een basis voor de kern: B=(1), dus dat betekent dat het beeld dimensie 3 moet hebben. Heeft het iets te maken met het feit dat je de vierdemachtsterm in functie van de tweedemachtsterm kunt schrijven (en hetzelf voor de derde en de eerste machtsterm) ?
Thanks
Re: Bepalen van beeld van een lineaire afbeelding
Dit lijkt me een notatie voor de afbeelding f van
polynomen van graad maximaal 3 = P3
op
polynomen van graad maximaal 4 = P4
Dus van:
 \;=\; a_3\cdot x^3 \;+\; a_2\cdot x^2 \;+\; a_1\cdot x \;+\; a_0)
op
 \;=\; b_4\cdot x^4 \;+\;b_3\cdot x^3 \;+\; b_2\cdot x^2 \;+\; b_1\cdot x \;+\; b_0)
Druk nu b0 t/m b4 elk uit in a0 t/m a3 (werk daarvoor het functievoorschrift uit).
Vervolgens kan je daarmee een 5 bij 4 matrix M opstellen, die vector a afbeeldt op b, in deze vorm:

Hiermee zou je beeld en kern moeten kunnen bepalen.
polynomen van graad maximaal 3 = P3
op
polynomen van graad maximaal 4 = P4
Dus van:
op
Druk nu b0 t/m b4 elk uit in a0 t/m a3 (werk daarvoor het functievoorschrift uit).
Vervolgens kan je daarmee een 5 bij 4 matrix M opstellen, die vector a afbeeldt op b, in deze vorm:
Hiermee zou je beeld en kern moeten kunnen bepalen.
Re: Bepalen van beeld van een lineaire afbeelding
Zit ik dan juist met het feit dat de basis voor de kern gewoon de verzameling met daarin 1 is?
Re: Bepalen van beeld van een lineaire afbeelding
is nog niet een volledige basis voor de kern.
Hoe ben je daaraan gekomen?
Re: Bepalen van beeld van een lineaire afbeelding
het voorschrift uitgewerkt in door overal de standaard derdegraadsvgl in te vullen, en dan gekeken wanneer die vierdegraadsvgl. 0 wordt. Als a=b=c=0 ,maar ik voel ook aan dat dit niet voldoende is...
Re: Bepalen van beeld van een lineaire afbeelding
Het gaat hier niet om de nulpunten van een 4e-graads vergelijking, maar om de vectoren uit P3(x) die op de nulvector in P4(x) worden afgebeeld.
We hadden
 \;=\; a_3\cdot x^3 \;+\; a_2\cdot x^2 \;+\; a_1\cdot x \;+\; a_0)
De machten van x:
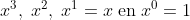
kan je zien als de 4 eenheidsvectoren van P3(x).
Elke derdegraadsvergelijking is een lineaire combinatie van die 4 vectoren.
Vergelijk dit met de eenheidsvectoren in een vierdimensionale vectorruimte.
Deze ruimte wordt opgespannen door deze vectoren.
Elke vector v in deze ruimte kan je uitdrukken als lineaire combinatie van deze eenheidsvectoren:
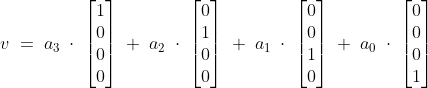
Hierbij zijn a3, a2, a1 en a0 scalaire constanten.
P3(x) wordt door f afgebeeld op P4(x):
 \;=\; b_4\cdot x^4 \;+\;b_3\cdot x^3 \;+\; b_2\cdot x^2 \;+\; b_1\cdot x \;+\; b_0)
Dit is een 5-dimensionale ruimte met eenheidsvectoren
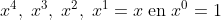
De afbeelding f van P3(x) naar P4(x) is een lineaire afbeelding, die beschreven kan worden door een matrix M, zodanig dat

Om deze matrix M te bepalen werken we eerst het functievoorschrift, gegeven door
) \;=\; x^2 P'(X) \;+\; x P''(X) \;+\; P'''(X) \;+\; (x^4+x^2+2)P'(0))
verder uit.
We hadden:
 \;=\; a_3\cdot x^3 \;+\; a_2\cdot x^2 \;+\; a_1\cdot x \;+\; a_0)
dus
 \;=\; 3a_3\cdot x^2 \;+\; 2a_2\cdot x \;+\; a_1)
 \;=\; 6a_3\cdot x \;+\; 2a_2)
etc.
Werk dit verder uit en combineer dit tot je kan schrijven
 \;=\; ...\cdot x^4 \;+\; ...\cdot x^3 \;+\; ...\cdot x^2 \;+\; ...\cdot x \;+\; ...)
volledig in coëfficiënten a0 t/m a3 uitgedrukt.
Kan je dan M bepalen?
Tenslotte moeten we (als we M hebben) om de kern te vinden nog oplossen:

We hadden
De machten van x:
kan je zien als de 4 eenheidsvectoren van P3(x).
Elke derdegraadsvergelijking is een lineaire combinatie van die 4 vectoren.
Vergelijk dit met de eenheidsvectoren in een vierdimensionale vectorruimte.
Deze ruimte wordt opgespannen door deze vectoren.
Elke vector v in deze ruimte kan je uitdrukken als lineaire combinatie van deze eenheidsvectoren:
Hierbij zijn a3, a2, a1 en a0 scalaire constanten.
P3(x) wordt door f afgebeeld op P4(x):
Dit is een 5-dimensionale ruimte met eenheidsvectoren
De afbeelding f van P3(x) naar P4(x) is een lineaire afbeelding, die beschreven kan worden door een matrix M, zodanig dat
Om deze matrix M te bepalen werken we eerst het functievoorschrift, gegeven door
verder uit.
We hadden:
dus
etc.
Werk dit verder uit en combineer dit tot je kan schrijven
volledig in coëfficiënten a0 t/m a3 uitgedrukt.
Kan je dan M bepalen?
Tenslotte moeten we (als we M hebben) om de kern te vinden nog oplossen:
Re: Bepalen van beeld van een lineaire afbeelding
Oh ja zo, bedankt dat is al veel duidelijker  ! En het beeld? Hoe ga je daar dan tewerk?
! En het beeld? Hoe ga je daar dan tewerk?
Re: Bepalen van beeld van een lineaire afbeelding
Als het goed is heb je nu gevonden:
 \;=\; (3a_3+a_1)\cdot x^4 \;+\; 2a_2\cdot x^3 \;+\; (6a_3+2a_1)\cdot x^2 \;+\; 2a_2\cdot x \;+\; (6a_3+2a_1))
waardoor

en elke beeldvector b geschreven kan worden als:
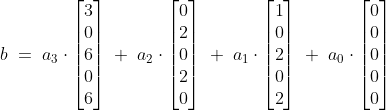
Kan je dit nog vereenvoudigen?
waardoor
en elke beeldvector b geschreven kan worden als:
Kan je dit nog vereenvoudigen?
Re: Bepalen van beeld van een lineaire afbeelding
laatste term valt weg
Re: Bepalen van beeld van een lineaire afbeelding
Klopt, en de derde is afhankelijk van de eerste twee, in dit geval simpelweg een veelvoud van de eerste.
Dus we houden over:
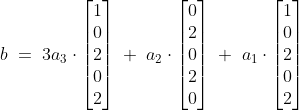
 \cdot \begin{bmatrix} 1\\0\\2\\0\\2\end{bmatrix} \;+\; 2a_2 \cdot \begin{bmatrix} 0\\1\\0\\1\\0\end{bmatrix})
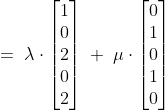
ofwel:
 \;+\; \mu \cdot(x^3 \;+\; x))
En wat had je gevonden voor de kern?
Komt dit overeen met de dimensiestelling?
Dus we houden over:
ofwel:
En wat had je gevonden voor de kern?
Komt dit overeen met de dimensiestelling?
Re: Bepalen van beeld van een lineaire afbeelding
a2 = 0 en a3= (-1/3)a1
Re: Bepalen van beeld van een lineaire afbeelding
Klopt.

Levert
a2 = 0
en
a3= (-1/3)a1
als we a1 = lambda nemen, dan is a3 = (-1/3)lambda
a2 moet nul zijn
a0 kunnen we vrij kiezen, stel mu:
dit levert
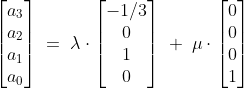
Herschrijf dit nog in termen van P3(x) en we zijn klaar.
Levert
a2 = 0
en
a3= (-1/3)a1
als we a1 = lambda nemen, dan is a3 = (-1/3)lambda
a2 moet nul zijn
a0 kunnen we vrij kiezen, stel mu:
dit levert
Herschrijf dit nog in termen van P3(x) en we zijn klaar.
Re: Bepalen van beeld van een lineaire afbeelding
Oke ja bedankt, ik vind de notatie wel wat verwarrend want wij hebben het anders geleerd (zonder matrixvorm)
Re: Bepalen van beeld van een lineaire afbeelding
Klopt. De weg hierboven is heel uitgebreid, om de link te leggen tussen de gebruikelijke matrix-vector-algebra en de iets minder bekende polynoom algebra Pn(x).
Hieronder een snellere weg:
[1] Bereik:
Voor het bereik kan je ook direct zeggen:
 \;=\; (3a_3+a_1)\cdot x^4 \;+\; 2a_2\cdot x^3 \;+\; (6a_3+2a_1)\cdot x^2 \;+\; 2a_2\cdot x \;+\; (6a_3+2a_1))
\cdot x^4 \;+\; (6a_3+2a_1)\cdot x^2 \;+\; (6a_3+2a_1) \;+\; 2a_2\cdot x^3 \;+\; 2a_2\cdot x)
\cdot (x^4 \;+\; 2\cdot x^2 \;+\; 2) \;+\; 2a_2\cdot(x^3 \;+\; x))
 \;+\; \mu \cdot (x^3 \;+\; x))
Met in de laatste stap
lambda = 3a3 + a1
en
mu = 2a2
[2] Kern:
En voor de kern:
 \;=\; (3a_3+a_1)\cdot x^4 \;+\; 2a_2\cdot x^3 \;+\; (6a_3+2a_1)\cdot x^2 \;+\; 2a_2\cdot x \;+\; (6a_3+2a_1) \;=\; 0)
betekent alle parameters 0, dus
3a3 + a1 = 0
en
2a2 = 0
Stel weer
a1 = lambda, dan is a3 = (-1/3)lambda
a2 moet nul zijn
a0 = mu
dan levert dit in P3(x):
 \;=\; a_3\cdot x^3 \;+\; a_2\cdot x^2 \;+\; a_1\cdot x \;+\; a_0)
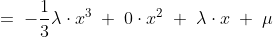
 \;+\; \mu)
Hieronder een snellere weg:
[1] Bereik:
Voor het bereik kan je ook direct zeggen:
Met in de laatste stap
lambda = 3a3 + a1
en
mu = 2a2
[2] Kern:
En voor de kern:
betekent alle parameters 0, dus
3a3 + a1 = 0
en
2a2 = 0
Stel weer
a1 = lambda, dan is a3 = (-1/3)lambda
a2 moet nul zijn
a0 = mu
dan levert dit in P3(x):
Re: Bepalen van beeld van een lineaire afbeelding
Zo had ik het oorspronkelijk ook geprobeerd, maar ik geraakte vast onderweg. Bedankt voor de hulp, Arie!

