Hallo allemaal,
ik moet voor Wiskunde D op school een soort "paragraaf" uit het boek maken over de hoofdstelling van de algebra.
Nu moet ik hier een stukje uitleg bij geven en 4 opdrachten met uitwerkingen maken.
Als ik op internet ga zoeken vind ik links en rechts wel wat dingen hierover maar niet veel.
Het stukje uitleg heb ik al wel kunnen maken aan de hand van wat informatie van internet.
Voor de opdrachten zou ik echter totaal niet weten wat ik zou kunnen doen.
Is er iemand die hier meer vanaf weet en die mij kan helpen met het verzinnen van deze opdrachten + uitwerkingen?
Alvast bedankt!
Hoofdstelling van de Algebra
Re: Hoofdstelling van de Algebra
Ik ben benieuwd naar "het stukje uitleg" ...Tieske123 schreef: Het stukje uitleg heb ik al wel kunnen maken aan de hand van wat informatie van internet.
Re: Hoofdstelling van de Algebra
Weet niet of het ergens op slaat maar ik ben benieuwd naar je reactie 
De hoofdstelling van de algebra is iets erg belangrijks binnen de wiskunde. Deze stelling zegt dat iedere veeltermige vergelijking waarvan n≥1 minstens één oplossing heeft.
Stel: is een veelterm van graad dan zijn er complexe getallen als:
zodat Het is duidelijk dat nulpunten zijn van p(z). Dit zijn dan ook ALLE nulpunten van p(z).
Het productis een ontbinding in lineaire factoren. De ontbinding is uniek voor een vergelijking, behalve de volgorde van de factoren, deze is bij iedere ontbinding van een veeltermige vergelijking hetzelfde.
De wortels vanhoeven niet allemaal anders te zijn, er kunnen ook dezelfde inzitten. Wel is het aantal factoren gelijk aan de graad van de veelterm, zo is te ontbinden in 2 factoren.
Ik weet zo niet hoe ik de formules uit open office hier kan laten zien maar het zijn eigenlijk de formules die je op deze site ook ziet: http://wortel.tue.nl/html/complex/complex.3.05.html
De hoofdstelling van de algebra is iets erg belangrijks binnen de wiskunde. Deze stelling zegt dat iedere veeltermige vergelijking waarvan n≥1 minstens één oplossing heeft.
Stel: is een veelterm van graad dan zijn er complexe getallen als:
zodat Het is duidelijk dat nulpunten zijn van p(z). Dit zijn dan ook ALLE nulpunten van p(z).
Het productis een ontbinding in lineaire factoren. De ontbinding is uniek voor een vergelijking, behalve de volgorde van de factoren, deze is bij iedere ontbinding van een veeltermige vergelijking hetzelfde.
De wortels vanhoeven niet allemaal anders te zijn, er kunnen ook dezelfde inzitten. Wel is het aantal factoren gelijk aan de graad van de veelterm, zo is te ontbinden in 2 factoren.
Ik weet zo niet hoe ik de formules uit open office hier kan laten zien maar het zijn eigenlijk de formules die je op deze site ook ziet: http://wortel.tue.nl/html/complex/complex.3.05.html
Re: Hoofdstelling van de Algebra
Ok, maar dat betekent dat je 'bekend' moet zijn met complexe getallen.
Kan je bv oplossen z³=1?
Verder moet je nog wat 'schaven' aan je zinnen ...
Met Latex kan je formules ingeven
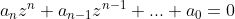
Kan je bv oplossen z³=1?
Verder moet je nog wat 'schaven' aan je zinnen ...
Met Latex kan je formules ingeven
Re: Hoofdstelling van de Algebra
Ja dat klopt, het zijn nu een beetje kromme zinnen, mede door het wegvallen van de formule's.
Ik ben redelijk bekend met complexe getallen, tenminste dat denk ik...
Maar die vergelijking die je daar geeft zou ik niet met complex kunnen oplossen.
Ik ben redelijk bekend met complexe getallen, tenminste dat denk ik...
Maar die vergelijking die je daar geeft zou ik niet met complex kunnen oplossen.
Re: Hoofdstelling van de Algebra
z³=1. je weet één opl dus, nu moet je je stelling toepassen ...Tieske123 schreef:Maar die vergelijking die je daar geeft zou ik niet met complex kunnen oplossen.
Re: Hoofdstelling van de Algebra
Kennis van complexe getallen is niet nodig om de hoofdstelling van de algebra weer te geven.
Hoofdstelling van de algebra:
Elke veelterm kan worden ontbonden in factoren van eerste of tweede graad (met reële coëfficienten).
Hoofdstelling van de algebra:
Elke veelterm kan worden ontbonden in factoren van eerste of tweede graad (met reële coëfficienten).



