Toepassing uitproduct
Re: Toepassing uitproduct
Nou, die hoek is onduidelijk. Theta dus die arctan(20/50), oftwel, de hoek tussen 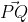 en de lijn vanaf P loodrecht op de Y-as (Y=25), of anders de lijn door Q, loodrecht op de Y-as (Y=5). Maar die specificeren ze niet expliciet, de afbeeldingen in mijn vraag zijn de enige waar ik beschikking over heb.
en de lijn vanaf P loodrecht op de Y-as (Y=25), of anders de lijn door Q, loodrecht op de Y-as (Y=5). Maar die specificeren ze niet expliciet, de afbeeldingen in mijn vraag zijn de enige waar ik beschikking over heb.
Re: Toepassing uitproduct
Ok, maar de berekeningen ...Rvo schreef:Nou, die hoek is onduidelijk. Theta dus die arctan(20/50), oftwel, de hoek tussenen de lijn vanaf P loodrecht op de Y-as (Y=25), of anders de lijn door Q, loodrecht op de Y-as (Y=5). Maar die specificeren ze niet expliciet, de afbeeldingen in mijn vraag zijn de enige waar ik beschikking over heb.
Maar hier heb je beslist iets over geleerd. De hoek theta die je noemt is onjuist.Nou, die hoek is onduidelijk.
Re: Toepassing uitproduct
Wat ik geleerd heb is dat ik het parallellogram moet nemen waarvan de PQ een schuine zijde is en vanuit Q is dan de andere schuine zijde. Dit lijkt ook op wat er in de oplossing staat: sin van de arctan van 20/50?
En die berekeningen zijn nou net het probleem, vector r is de grote onbekende?
En die berekeningen zijn nou net het probleem, vector r is de grote onbekende?
Re: Toepassing uitproduct
Nee hoor, je kan r=(-100,25,0) nemen.Rvo schreef: En die berekeningen zijn nou net het probleem, vector r is de grote onbekende?
F en r liggen in het xy-vlak (z=0). F kan je ontbinden evenwijdig aan x- en y-as, dat zijn de componenten, en daarvan het moment tov O bepalen.
Over je hoek theta heb ik al gezegd dat deze fout is.
Re: Toepassing uitproduct
Ik heb 750 gevonden.
Ik heb F naar de O gelegd, dus F = (-50, 20, 0). De r blijft inderdaad (-100, 25, 0).
Theta is de hoek tussen F en r, bij O dus.
 = \frac{\vec{r} \cdot \vec{F}}{\left | \vec{r} \right | \cdot \left | \vec{F} \right |})
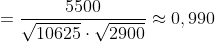
Wat betekent dat:
 = \sqrt{1-(0,99)^2} = \approx 0,13511) (omgewerkt vanuit
(omgewerkt vanuit ^2 + sin(\alpha)^2 = 1) )
)
Dan heb je het parallellogram waarvan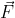 de onderste zijde is. Voor het verkrijgen van de oppervlakte moet je dan de opstaande rand nemen als hoogte van de rechthoek die gelijk is aan het paralellogram (lekkere worodkeuze?) en die is:
de onderste zijde is. Voor het verkrijgen van de oppervlakte moet je dan de opstaande rand nemen als hoogte van de rechthoek die gelijk is aan het paralellogram (lekkere worodkeuze?) en die is:
)
De oppervlakte wordt dan:
) = \sqrt{10625} \cdot (\sqrt{2900} \cdot 0,1351132) = 750)
Alleen waar komt in godsnaam die 37,5 vandaan dan in hun oplossing? Iets met r verleggen weg van de O ipv van F náár de O leggen?
Is mijn gedachtengang nu goed?
Ik heb F naar de O gelegd, dus F = (-50, 20, 0). De r blijft inderdaad (-100, 25, 0).
Theta is de hoek tussen F en r, bij O dus.
Wat betekent dat:
Dan heb je het parallellogram waarvan
De oppervlakte wordt dan:
Alleen waar komt in godsnaam die 37,5 vandaan dan in hun oplossing? Iets met r verleggen weg van de O ipv van F náár de O leggen?
Is mijn gedachtengang nu goed?
Re: Toepassing uitproduct
Zo kan het, maar kan je het uitproduct niet bepalen?
Dus:
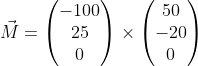
En de berekening met de componenten?
Dus:
En de berekening met de componenten?
Re: Toepassing uitproduct
Met dat uitproduct kom ik ook op 750. Waarom mag F ook daar liggen? Als ik dan F neem heb ik de wortel van 2900, neem ik theta als sin(arctan(20/50)) alleen moet r dan 37.5 zijn dus en die haal ik er nog steeds niet uit... Geen ene vector lijkt zo lang te zijn.. 25/2+25? Echt geen idee. En hoe bedoel je componenten? Bedankt 
Re: Toepassing uitproduct
Hoe bereken je het uitproduct?Rvo schreef:Met dat uitproduct kom ik ook op 750. Waarom mag F ook daar liggen?
Je weet dat je een kracht langs z'n werklijn kunt verplaatsen. Bereken het uitproduct nu ook met r=(-50,5,0)?
En hoe bedoel je componenten?
Heb je nog niet eerder een kracht ontbonden in componenten? Dat klinkt heel vreemd ...
Ik zou hier niet mee verder gaan. Ga nog eens andere vb na, dat lijkt me zinneger...Als ik dan F neem heb ik de wortel van 2900, neem ik theta als sin(arctan(20/50)) alleen moet r dan 37.5 zijn dus en die haal ik er nog steeds niet uit... Geen ene vector lijkt zo lang te zijn.. 25/2+25? Echt geen idee.
Re: Toepassing uitproduct
SafeX schreef:Hoe bereken je het uitproduct?Rvo schreef:Met dat uitproduct kom ik ook op 750. Waarom mag F ook daar liggen?
Je weet dat je een kracht langs z'n werklijn kunt verplaatsen. Bereken het uitproduct nu ook met r=(-50,5,0)?
Zal ik doen, een gok is dat dit hetzelfde zal geven?
En hoe bedoel je componenten?
Heb je nog niet eerder een kracht ontbonden in componenten? Dat klinkt heel vreemd ...
Hangt er van af. Ik weet wel dat een vector componenten heeft. Het begrip 'kracht' kwam eigenlijk alleen naar voren als 'toepassing van het uitproduct'.
Re: Toepassing uitproduct
Zal ik doen, een gok is dat dit hetzelfde zal geven?SafeX schreef: Hoe bereken je het uitproduct?
Je weet dat je een kracht langs z'n werklijn kunt verplaatsen. Bereken het uitproduct nu ook met r=(-50,5,0)?
Hangt er van af. Ik weet wel dat een vector componenten heeft. Het begrip 'kracht' kwam eigenlijk alleen naar voren als 'toepassing van het uitproduct'. Blijkbaar kan een vector veel voorstellen, waaronder een kracht.Heb je nog niet eerder een kracht ontbonden in componenten? Dat klinkt heel vreemd ...
Re: Toepassing uitproduct
Bedoel je hier misschien de kentallen? Zo ja, dat is niet hetzelfde.Ik weet wel dat een vector componenten heeft.
Dat is wel heel magertjes ...Het begrip 'kracht' kwam eigenlijk alleen naar voren als 'toepassing van het uitproduct'.
Elke vector is te zien als resultante van twee of meer vectoren, bv
als a en b vectoren zijn; a+b=c, dan is c de som, ook wel de resultante, van a en b.
Deze kracht F kan je vanuit het punt (-100,25,0) ontbinden evenwijdig aan de x- en y-as zodanig dat Fx+Fy=F.
Probeer dat eens en bepaal de grootte.
Ben je bekend met het begrip: moment M van een kracht F tov van een punt P is het product van de kracht met de afstand d tot het punt P: dus F*d=M.
Wat heeft dit te maken met het uitproduct van F en d?
Re: Toepassing uitproduct
Het boek behandelt vectoren, die hele kracht is slechts een bijproduct denk ik. Met componenten bedoelde ik de x, y en z, verder ging het niet. Het is maar een basisboek dus ik zou er niet teveel achter zoeken. In ieder geval bedankt voor de inzichten 
Re: Toepassing uitproduct
Het boek ... , welk boek? Dat het hier als vb om krachten gaat is duidelijk, maar dat betekent wel dat je dan de achtergrond hiervan moet kennen.Rvo schreef:Het boek behandelt vectoren, die hele kracht is slechts een bijproduct denk ik. Met componenten bedoelde ik de x, y en z, verder ging het niet. Het is maar een basisboek dus ik zou er niet teveel achter zoeken. In ieder geval bedankt voor de inzichten
Verder heb ik je laten zien dat je vectoren kunt optellen, bij krachten betekent dit samenstellen. En bij vector v(a,b,c) zijn a, b en c de kentallen

