Voor een productreeks moeten we de minimale diameter (d) van een pin berekenen.
De formule voor het controleren van de pin is hieronder weergegeven:
(M/((x∙((π∙d^3)/y)∙f_y)/γ_M0 ))^2+(F/((y∙(z∙π∙d^2 )∙f_u)/γ_M2 ))^2=1
Kan iemand me helpen deze formule om te bouwen, zodat de minimale diameter (d) kan worden berekend?
Bij voorbaat bedankt.
Joeri
Minimale diameter pin
Re: Minimale diameter pin
Je hebt (iets anders geschreven):
Vermenigvuldig teller en noemer van de 2 breuken met g_M0 resp. g_M2:
Vermenigvuldig teller en noemer van de eerste breuk met y:
Isoleer d uit de kwadraten:
Definieer
P = ( M*g_M0*y / (x*pi*f_y) )^2
Q = ( F*g_M2 / (y*z*pi*f_u) )^2
dan houden we over:
P*(1/d^6) + Q*(1/d^4) = 1
ofwel (vermenigvuldig links en rechts met d^6):
P + Q*d^2 = d^6
ofwel
d^6 - Q*d^2 - P = 0
Stel x = d^2 dan houden we over:
x^3 - Q*x - P = 0
met P en Q bekend (zie hierboven).
Dit is een derdegraads vergelijking in x, lukt het je om x hieruit op te lossen?
Code: Selecteer alles
( M / ( (x*((pi*d^3)/y) *f_y) /g_M0 ) )^2
+
( F / ( (y* (z*pi*d^2) *f_u) /g_M2 ) )^2
=
1Code: Selecteer alles
( M*g_M0 / (x*((pi*d^3)/y) *f_y) )^2
+
( F*g_M2 / (y* (z*pi*d^2) *f_u) )^2
=
1Code: Selecteer alles
( M*g_M0*y / (x*pi*d^3*f_y) )^2
+
( F*g_M2 / (y*z*pi*d^2*f_u) )^2
=
1Code: Selecteer alles
( M*g_M0*y / (x*pi*f_y) )^2 * ( 1 / d^3 )^2
+
( F*g_M2 / (y*z*pi*f_u) )^2 * ( 1 / d^2)^2
=
1P = ( M*g_M0*y / (x*pi*f_y) )^2
Q = ( F*g_M2 / (y*z*pi*f_u) )^2
dan houden we over:
P*(1/d^6) + Q*(1/d^4) = 1
ofwel (vermenigvuldig links en rechts met d^6):
P + Q*d^2 = d^6
ofwel
d^6 - Q*d^2 - P = 0
Stel x = d^2 dan houden we over:
x^3 - Q*x - P = 0
met P en Q bekend (zie hierboven).
Dit is een derdegraads vergelijking in x, lukt het je om x hieruit op te lossen?
Re: Minimale diameter pin
Bedankt Arie voor het snelle antwoord.
Het oplossen van een derdegraads vergelijking zou normaal gesproken moeten lukken.
Ik zie echter dat ik type fout heb gemaakt in de input:
(M/((x∙((π∙d^3)/y)∙f_y)/γ_M0 ))^2+(F/((kk∙(z∙π∙d^2 )∙f_u)/γ_M2 ))^2=1
De factor y in het tweede deel van de formule is een andere variabele dan de y-waarmee in het eerste deel wordt gedeeld. Wat zijn de implicaties hiervan?
Joeri
Het oplossen van een derdegraads vergelijking zou normaal gesproken moeten lukken.
Ik zie echter dat ik type fout heb gemaakt in de input:
(M/((x∙((π∙d^3)/y)∙f_y)/γ_M0 ))^2+(F/((kk∙(z∙π∙d^2 )∙f_u)/γ_M2 ))^2=1
De factor y in het tweede deel van de formule is een andere variabele dan de y-waarmee in het eerste deel wordt gedeeld. Wat zijn de implicaties hiervan?
Joeri
Re: Minimale diameter pin
Ter verduidelijking:
De juiste formule zou moeten zijn:
(M/((x∙((π∙d^3)/y)∙f_y)/γ_M0 ))^2+(F/((k∙(z∙π∙d^2 )∙f_u)/γ_M2 ))^2=1
De juiste formule zou moeten zijn:
(M/((x∙((π∙d^3)/y)∙f_y)/γ_M0 ))^2+(F/((k∙(z∙π∙d^2 )∙f_u)/γ_M2 ))^2=1
Re: Minimale diameter pin
Als het goed is wordt het nu deze formule:
} \right)^2 + \left( \frac{F}{\left(\frac{k\cdot z \cdot \pi \cdot d^2 \cdot f_u}{\gamma_{M2}} \right) } \right)^2 = 1)
ofwel (vermenigvuldig teller en noemer van de linker breuk met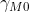 en die van de rechter breuk met
en die van de rechter breuk met 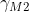 ):
):
^2 + \left( \frac{F\cdot \gamma_{M2}}{k\cdot z \cdot \pi \cdot d^2 \cdot f_u } \right)^2 = 1)
ofwel (vermenigvuldig teller en noemer van de linker breuk met y):
^2 + \left( \frac{F\cdot \gamma_{M2}}{k\cdot z \cdot \pi \cdot d^2 \cdot f_u } \right)^2 = 1)
ofwel (haal de machten van d naar buiten):
^2\cdot d^{-6} + \left( \frac{F\cdot \gamma_{M2}}{k\cdot z \cdot \pi \cdot f_u } \right)^2 \cdot d^{-4} = 1)
ofwel (vermenigvuldig links en rechts met d^6):
^2 + \left( \frac{F\cdot \gamma_{M2}}{k\cdot z \cdot \pi \cdot f_u } \right)^2 \cdot d^2 = d^6)
ofwel (herschik de vergelijking):
^2 \cdot d^2 - \left( \frac{y \cdot M \cdot \gamma_{M0}}{x \cdot \pi \cdot f_y} \right)^2 = 0)
ofwel

met
^2)
en
^2)
en als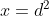 :
:

Los x (numeriek) op, dan is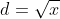
ofwel (vermenigvuldig teller en noemer van de linker breuk met
ofwel (vermenigvuldig teller en noemer van de linker breuk met y):
ofwel (haal de machten van d naar buiten):
ofwel (vermenigvuldig links en rechts met d^6):
ofwel (herschik de vergelijking):
ofwel
met
en
en als
Los x (numeriek) op, dan is
Re: Minimale diameter pin
Bedankt voor de hulp.

