Hallo ik zit vast met een wiskunde oefening. Kan er iemand mij helpen. / staat voor een breuk.
Dit is de oefening. Ik heb er al een beetje van kunnen oplossen maar nu zit ik vast.
x²+ y² = 25
4x -3y = 0
__________
x² + y² = 25
x = 3/4y
__________
(3/4y)² + y² = 25
x = 3/4y
__________
?
stelsels van vergelijkingen
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: stelsels van vergelijkingen
Merk op dat ^2=\frac{9}{16}y^2) , dus
, dus 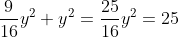 , dus
, dus 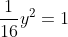 , dus y² = 16, dus y = ... of y = ...,
, dus y² = 16, dus y = ... of y = ...,
dus x = ... of x = ...
dus x = ... of x = ...
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: stelsels van vergelijkingen
Bedankt voor je antwoord Arno.
Maar Kan je me vertellen hoe je van 9/16y² + y² naar 25/16y² komt.
Alvast bedankt.
Maar Kan je me vertellen hoe je van 9/16y² + y² naar 25/16y² komt.
Alvast bedankt.
Re: stelsels van vergelijkingen
9y²/16 + y² = 9y²/16 + 1*y² = 9y²/16 + 16y²/16 = (9 + 16)y² / 16 = 25y²/16. Okay?
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: stelsels van vergelijkingen
Een dikke merci David.

