Beste mensen,
Stel je werpt N dobbelstenen, waarbij elke dobbelsteen Y vlakken heeft met waarden {1, 2,…., Y}. Je wilt nu weten wat de kans p is op elke afzonderlijke somscore S. Die kansverdeling lijkt “normaal verdeeld” met gemiddelde ((Y+1)*N)/2. Gegeven Y en N, is er een formule die p(S) bepaald?
Het antwoord op deze vraag heb ik nodig in verband met een probleem dat ik heb met een non-parametrische toets die ik wil generaliseren, wanneer je werkt met N schaalvragen en Y antwoordcategorieën en je wilt weten wat de kans is van een zekere somscore t.o.v. random antwoorden.
Alvast hartelijk dank, Erwin
Kansverdeling somscores
Re: Kansverdeling somscores
Het totaal aantal mogelijke uitkomsten U van een worp met n dobbelstenen elk met y vlakken is
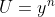
Definieer C = het aantal uitkomsten waarbij je in totaal S ogen gooit.
De kans op S ogen is dan
 = \frac{C}{U})
Nu is C de coëfficiënt van x^S in de uitwerking van
^n)
Via formele machtreeksen kan je afleiden dat
 = \sum_{i=0}^\infty (-1)^i \cdot {S-1-y \cdot i \choose S-n-y\cdot i} \cdot {n \choose i})
Voorbeeld:
Je hebt n=8 dobbelstenen met elk y=5 vlakken.
Je wilt weten op hoeveel manieren je hiermee S=24 kan gooien.
copy/paste
(x+x^2+x^3+x^4+x^5)^8
naar http://www.wolframalpha.com/
en je krijgt (naast een boel andere gegevens) als expanded form:
x^40 + 8 x^39 + 36 x^38 + 120 x^37 + 330 x^36 + 784 x^35 + 1652 x^34 +
3144 x^33 + 5475 x^32 + 8800 x^31 + 13140 x^30 + 18320 x^29 + 23940 x^28 +
29400 x^27 + 34000 x^26 + 37080 x^25 + 38165 x^24 + 37080 x^23 + 34000 x^22 +
29400 x^21 + 23940 x^20 + 18320 x^19 + 13140 x^18 + 8800 x^17 + 5475 x^16 +
3144 x^15 + 1652 x^14 + 784 x^13 + 330 x^12 + 120 x^11 + 36 x^10 + 8 x^9 + x^8
De coëfficiënt van x^24 = 38165, dus je kan op 38165 manieren 24 gooien.
Via de formule kan je ook direct uitrekenen:
 = {23 \choose 16} \cdot {8 \choose 0} - {18 \choose 11} \cdot {8 \choose 1} + {13 \choose 6} \cdot {8 \choose 2} - {8 \choose 1} \cdot {8 \choose 3})
(alle overige termen zijn nul)
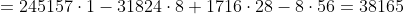
Definieer C = het aantal uitkomsten waarbij je in totaal S ogen gooit.
De kans op S ogen is dan
Nu is C de coëfficiënt van x^S in de uitwerking van
Via formele machtreeksen kan je afleiden dat
Voorbeeld:
Je hebt n=8 dobbelstenen met elk y=5 vlakken.
Je wilt weten op hoeveel manieren je hiermee S=24 kan gooien.
copy/paste
(x+x^2+x^3+x^4+x^5)^8
naar http://www.wolframalpha.com/
en je krijgt (naast een boel andere gegevens) als expanded form:
x^40 + 8 x^39 + 36 x^38 + 120 x^37 + 330 x^36 + 784 x^35 + 1652 x^34 +
3144 x^33 + 5475 x^32 + 8800 x^31 + 13140 x^30 + 18320 x^29 + 23940 x^28 +
29400 x^27 + 34000 x^26 + 37080 x^25 + 38165 x^24 + 37080 x^23 + 34000 x^22 +
29400 x^21 + 23940 x^20 + 18320 x^19 + 13140 x^18 + 8800 x^17 + 5475 x^16 +
3144 x^15 + 1652 x^14 + 784 x^13 + 330 x^12 + 120 x^11 + 36 x^10 + 8 x^9 + x^8
De coëfficiënt van x^24 = 38165, dus je kan op 38165 manieren 24 gooien.
Via de formule kan je ook direct uitrekenen:
(alle overige termen zijn nul)
Re: Kansverdeling somscores
Uitstekend. Dankjewel!

