Hallo,
Ik ben nieuw hier. Ik heb zelf geprobeerd mijn oplossing te vinden, maar liep tegen mijn beperkte wiskundige kennis aan. Ik hoop dat een van jullie kan helpen.
Het gaat om het volgende:
Ik wil een functie die (school)cijfers kan berekenen op basis van behaalde punten. Vaak wordt dan de functie "punten/maximum x 9 + 1" gebruikt. Het nadeel hiervan is dat de cesuur (het percentage van de punten wanneer een voldoende wordt gehaald) altijd op 50% ligt. Oftewel: als een leerling de helft van de punten heeft, krijgt hij een 5.5 (de helft van 9=4.5 +1)
Deze functie geeft een lineaire lijn.
Ik wil echter een kromme lijn, zodat de eerste paar punten minder zwaar wegen dan de laatste paar punten. Hoe meer punten een leerling dus haalt, hoe sneller zijn cijfer omhoog gaat.
Met een minimum cijfer van 1 en maximum van 10 en minimum aantal punten van 0 en maximum van 25, heb ik deze functie gemaakt: ( ( 10^(1/25) ) ^ x). Dit geeft een mooie exponentiele functie die precies doet wat ik wil...
MAAR, ik wil kunnen bepalen door welk punt de grafiek gaat bij y=5.5 (de voldoende-grens) De ene toets moet namelijk een cesuur hebben van 50% (rechte lijn) en een makkelijkere toets moet een hogere cesuur hebben, bijvoorbeeld van 75%.
In het voorbeeld gaat de grafiek door punt (18.5, 5.5), dus hier ligt de cesuur bij 18.5 punten (74% van 25 punten).
Kan iemand bedenken hoe je een functie moet maken bij verschillende cesuren (y=5.5)?
Een lastige vraag, daar ben ik me van bewust. Als er meer uitleg nodig is, dan hoor ik dat graag.
Groeten, Eduard
Perfecte cijferberekening gezocht
Re: Perfecte cijferberekening gezocht
Hangt ervan af wat je van de functie weet. Misschien kan je een algebraïsche oplossing vinden. Anders kan je nog de bissectiemethode gebruiken (aangenomen dat meer punten betekent een hoger cijfer betekent). Je zoekt dan x zodat c(x) - 5.5 = 0, waar c het cijfer geeft dat hoort bij het aantal punten x. Mogelijk wil je x nog afronden, bijvoorbeeld als je gevonden oplossing niet geheel is.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: Perfecte cijferberekening gezocht
Een mogelijke oplossing is dat je je formule uitbreidt naar deze:
 = 1 + \frac{9 \cdot (10^{c \cdot x/m}-1)}{10^c - 1})
Hierin is
f(x) = het behaalde cijfer bij x punten
m = het maximaal te behalen punten
c = een te bepalen constante

In dit plaatje is f(x) geplot voor m=25 en een aantal waarden voor c:
c = 0.21049 (blauw)
c = 0.51385 (groen)
c = 1 (rood)
c = 1.42504 (paars)
c = 3.76194 (lichtgroen)
In zwart zie je bovendien
- de horizontale lijn f(x) = 5.5
- en de schuine lijn van de lineaire cesuur
Voor c = 1 gaat bovenstaande formule over in de formule die jij gaf:
 = 1 + \frac{9 \cdot (10^{1 \cdot x/m}-1)}{10^1 - 1})
}{10 - 1})
}{9})
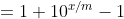
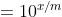
^x)
en voor m = 25:
^x)
Dit is de rode kromme in de grafiek.
Voor elke gewenste cesuur in punten kan nu je de bijbehorende waarde van c bepalen uit:
}{10^c - 1} = 5.5)
Voorbeeld:
Stel we willen de cesuur bij 80% leggen.
Als we maximaal m=25 punten kunnen halen, moet x = 0.80 * 25 = 20 punten dus het cijfer 5.5 opleveren.
Ofwel: in dit geval moet x/m = 0.80 zijn.
We zoeken nu de c waarvoor
}{10^c - 1} = 5.5)
Deze vergelijking kan je oplossen met de methode van David hierboven,
of je copy/paste de volgende lijn:
1+9*(10^(c*0.80)-1)/(10^c-1)=5.5
naar het invoerveld van http://www.wolframalpha.com/
Dit programma doet dan het rekenwerk voor je, en geeft als antwoord (onder "Solution" of "Numerical solution"):
c = 1.42504
bij een cesuur van 80% en m=25 kan je het behaalde cijfer f(x) dus berekenen via
 = 1 + \frac{9 \cdot (10^{1.42504 \cdot x/25}-1)}{10^{1.42504} - 1})
In onderstaande tabel staan voor deze formule:
x = aantal punten
f(x) = behaalde cijfer
toename = toename van het cijfer ten opzichte van het cijfer bij 1 punt minder (= de f(x) van de vorige regel)
Je ziet dat elk extra behaald punt steeds meer waard wordt voor je cijfer (de toename wordt steeds groter).
In de grafiek bovenaan in deze post ben ik uitgegaan van
cesuur = 56% => x/m = 0.56 => c = 0.21049 (blauw)
cesuur = 64% => x/m = 0.64 => c = 0.51385 (groen)
cesuur = 80% => x/m = 0.80 => c = 1.42504 (paars)
cesuur = 92% => x/m = 0.92 => c = 3.76194 (lichtgroen)
voor m=25 zijn dit resp. 14, 16, 20 en 23 punten.
Hierin is
f(x) = het behaalde cijfer bij x punten
m = het maximaal te behalen punten
c = een te bepalen constante

In dit plaatje is f(x) geplot voor m=25 en een aantal waarden voor c:
c = 0.21049 (blauw)
c = 0.51385 (groen)
c = 1 (rood)
c = 1.42504 (paars)
c = 3.76194 (lichtgroen)
In zwart zie je bovendien
- de horizontale lijn f(x) = 5.5
- en de schuine lijn van de lineaire cesuur
Voor c = 1 gaat bovenstaande formule over in de formule die jij gaf:
en voor m = 25:
Dit is de rode kromme in de grafiek.
Voor elke gewenste cesuur in punten kan nu je de bijbehorende waarde van c bepalen uit:
Voorbeeld:
Stel we willen de cesuur bij 80% leggen.
Als we maximaal m=25 punten kunnen halen, moet x = 0.80 * 25 = 20 punten dus het cijfer 5.5 opleveren.
Ofwel: in dit geval moet x/m = 0.80 zijn.
We zoeken nu de c waarvoor
Deze vergelijking kan je oplossen met de methode van David hierboven,
of je copy/paste de volgende lijn:
1+9*(10^(c*0.80)-1)/(10^c-1)=5.5
naar het invoerveld van http://www.wolframalpha.com/
Dit programma doet dan het rekenwerk voor je, en geeft als antwoord (onder "Solution" of "Numerical solution"):
c = 1.42504
bij een cesuur van 80% en m=25 kan je het behaalde cijfer f(x) dus berekenen via
In onderstaande tabel staan voor deze formule:
x = aantal punten
f(x) = behaalde cijfer
toename = toename van het cijfer ten opzichte van het cijfer bij 1 punt minder (= de f(x) van de vorige regel)
Je ziet dat elk extra behaald punt steeds meer waard wordt voor je cijfer (de toename wordt steeds groter).
Code: Selecteer alles
x f(x) toename
0: 1.0000
1: 1.0493 0.04929
2: 1.1055 0.05620
3: 1.1696 0.06409
4: 1.2426 0.07307
5: 1.3260 0.08332
6: 1.4210 0.09501
7: 1.5293 0.10833
8: 1.6528 0.12353
9: 1.7937 0.14085
10: 1.9543 0.16061
11: 2.1374 0.18313
12: 2.3463 0.20882
13: 2.5844 0.23811
14: 2.8559 0.27150
15: 3.1654 0.30958
16: 3.5184 0.35300
17: 3.9210 0.40251
18: 4.3799 0.45897
19: 4.9033 0.52334
20: 5.5000 0.59674
21: 6.1804 0.68043
22: 6.9563 0.77587
23: 7.8410 0.88468
24: 8.8498 1.00877
25: 10.0000 1.15025cesuur = 56% => x/m = 0.56 => c = 0.21049 (blauw)
cesuur = 64% => x/m = 0.64 => c = 0.51385 (groen)
cesuur = 80% => x/m = 0.80 => c = 1.42504 (paars)
cesuur = 92% => x/m = 0.92 => c = 3.76194 (lichtgroen)
voor m=25 zijn dit resp. 14, 16, 20 en 23 punten.
Re: Perfecte cijferberekening gezocht
Heel erg bedankt voor de uitgebreide uitleg en de aangedragen oplossing. Dit is vrijwel exact waar ik naar op zoek was!
Ik kan hier nu verder mee aan de slag om op een mooie manier cijfers te berekenen.
Groeten, Eduard
Ik kan hier nu verder mee aan de slag om op een mooie manier cijfers te berekenen.
Groeten, Eduard

