Hallo,
Ik heb de volgende formule:
Y = (42,4 * LG^0,75 + 442 * X ) * (1+(X-15)*0,00165)
k weet Y, Hoe kan ik de formule ombouwen zodat ik met Y, X kan berekenen
Ik was zelf begonnen met het onderstaande, alleen kom ik er zelf verder niet uit:
Y = (42,4 * LG^0,75 + 442 * X ) * (0,97525 + 0,00165 * X)
Ik wil dus Y invullen dus bijv.
Y = 5313,127
Y = 12088,217
waardoor ik als antwoord krijg:
x=0
x= 15
M.v.g.
Guus
Formule ombouwen
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Formule ombouwen
Laten we eerst eens 0,00165(X-15) eens uitwerken. Dit geeft: 0,00165(x-15) = 0,00165X-0,02475. De formule is dus te herschrijven als (0,00165X-0,02475)=0,7293X^2+(0,06996LG^{0,75}-10,9395)X-1,0494LG^{0,75}) . Je hebt nu een uitdrukking van de vorm Y = aX²+bX+c. Nu geldt dat
. Je hebt nu een uitdrukking van de vorm Y = aX²+bX+c. Nu geldt dat ^2-\frac{b^2-4ac}{4a}) , dus
, dus ^2=\frac{Y}{a}+\frac{b^2-4ac}{4a^2}) , dus
, dus ^2=\frac{4aY+b^2-4ac}{4a^2}) , dus
, dus 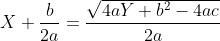 of
of 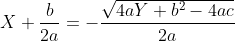 , dus
, dus 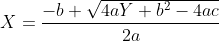 of
of 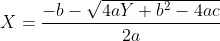 of
of 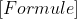 .
.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Formule ombouwen
Laten we eerst eens 0,00165(X-15) eens uitwerken. Dit geeft: 0,00165(x-15) = 0,00165X-0,02475. De formule is dus te herschrijven als (0,00165X-0,02475)=0,7293X^2+(0,06996LG^{0,75}-10,9395)X-1,0494LG^{0,75}) .
.
Je hebt nu een uitdrukking van de vorm Y = aX²+bX+c. Nu geldt dat^2-\frac{b^2-4ac}{4a}) , dus
, dus ^2=\frac{Y}{a}+\frac{b^2-4ac}{4a^2}) , dus
, dus ^2=\frac{4aY+b^2-4ac}{4a^2}) , dus
, dus 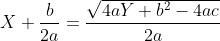 of
of 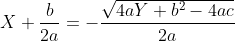 , dus
, dus 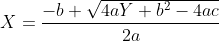 of
of 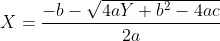 .
.
Je hebt nu een uitdrukking van de vorm Y = aX²+bX+c. Nu geldt dat
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Formule ombouwen
Als LG een constante is, hier LG = 648.37
dan wordt de vergelijking die je zelf al gevonden had:
\(y = (42.4 * 648.37^{0.75} + 442 * x ) * (0.97525 + 0.00165 * x)\)
ofwel
\(y = (5447.95 + 442*x) * (0.97525 + 0.00165*x)\)
ofwel
\(y = 0.72930*x^2 + 440.050*x + 5313.11\)
ofwel
\(0.72930*x^2 + 440.050*x + (5313.11 - y) = 0\)
Gebruik nu de abc-formule zoals arno hierboven beschreef met:
a = 0.72930
b = 440.050
c = 5313.11 - y
waarmee je voor elke waarde van y nu 2 oplossingen voor x zal vinden, waarvan er 1 de juiste is.
Kom je hiermee verder?
dan wordt de vergelijking die je zelf al gevonden had:
\(y = (42.4 * 648.37^{0.75} + 442 * x ) * (0.97525 + 0.00165 * x)\)
ofwel
\(y = (5447.95 + 442*x) * (0.97525 + 0.00165*x)\)
ofwel
\(y = 0.72930*x^2 + 440.050*x + 5313.11\)
ofwel
\(0.72930*x^2 + 440.050*x + (5313.11 - y) = 0\)
Gebruik nu de abc-formule zoals arno hierboven beschreef met:
a = 0.72930
b = 440.050
c = 5313.11 - y
waarmee je voor elke waarde van y nu 2 oplossingen voor x zal vinden, waarvan er 1 de juiste is.
Kom je hiermee verder?

