Pagina 1 van 1
Stelsel oplossen met product van onbekenden
Geplaatst: 18 apr 2020, 09:25
door Dorian
Hallo,
Hoe zou je zo'n stelsel algebraïsch kunnen oplossen?
Alvast bedankt!
https://imgur.com/gallery/VUGby0n
Re: Stelsel oplossen met product van onbekenden
Geplaatst: 18 apr 2020, 15:44
door arno
Stel
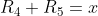
dan is de eerste vergelijking te schrijven als
=x\cdot R_6)
, dus
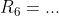
Uit
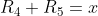
volgt dat
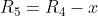
en
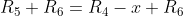
, dus de tweede vergelijking is net als de derde vergelijking uit te drukken in
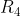
en x. Los nu het stelsel op dat bestaat uit de tweede en de derde vergelijking, waarbij
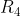
en x de onbekenden zijn.
Re: Stelsel oplossen met product van onbekenden
Geplaatst: 18 apr 2020, 19:12
door SafeX
Hoe ben je aan deze vergelijkingen gekomen?
Met de gegeven weerstanden is er geen oplossing voor R4, R5 en R6.
Re: Stelsel oplossen met product van onbekenden
Geplaatst: 18 apr 2020, 21:23
door arie
Met het schema van arno kom ik uit op
R4 = 272533 / 1530 ~= 178.12614
R5 = 2997863 / 16930 ~= 177.07401
R6 = 272533 / 40 = 6813.325
Re: Stelsel oplossen met product van onbekenden
Geplaatst: 20 apr 2020, 15:54
door SafeX
Dag Arie, bedankt voor je reactie.
De berekening nog eens nagelopen en jouw antwoorden kloppen,
Het venijn zat in het feit dat als we R4+R5+R6=R stellen, R6>R/2, terwijl R4<R/2 en R5<R/2.
Overigens ben ik benieuwd naar jouw berekening.
Re: Stelsel oplossen met product van onbekenden
Geplaatst: 21 apr 2020, 21:36
door arie
Mijn oplossing is veel omslachtiger dan die van arno, en gaat bovendien wat ver voor een vrij eenvoudig natuurkunde / elektronica vraagstuk.
Hier In ieder geval mijn route:
Het stelsel in een iets andere beschrijving:
\(\left\{\begin{matrix} a(r+s+t) & = & t(r+s)\\ b(r+s+t) & = & r(s+t)\\ c(r+s+t) & = & s(r+t) \end{matrix}\right.\)
ofwel
\(\left\{\begin{matrix} ar+as+at & = & rt+st\\ br+bs+bt & = & rs+rt\\ cr+cs+ct & = & rs+st \end{matrix}\right.\)
Los dit stelsel op naar r, s en rs:
\(\left\{\begin{matrix} (a-t)r &+&(a-t)s& & & = & -at\\ (b-t)r&+&bs &-&rs & = & -bt\\ cr&+&(c-t)s &-&rs & = & -ct \end{matrix}\right.\)
en de oplossingsvector v is:
\(\text{v} = \begin{bmatrix} a-t & a-t & 0\\ b-t & b & -1\\ c & c-t & -1 \end{bmatrix}^{-1} \cdot \begin{bmatrix} -at\\-bt\\ -ct \end{bmatrix}\)
Nu zijn s, r en sr uitgedrukt in ( t en de constanten a, b en c ).
Uit s * r = sr ofwel v[1] * v[2] - v[3] = 0 volgt dan t:
\(t = \frac{a^2+b^2+c^2-2(ab+ac+bc)}{2(a-b-c)}\)
en uit t (en a, b en c) volgen r = v[1] en s = v[2].
Re: Stelsel oplossen met product van onbekenden
Geplaatst: 22 apr 2020, 10:19
door arie
En hier de volledige uitwerking via de methode van arno:
\(\left\{\begin{matrix} a(r+s+t) & = & t(r+s)\\ b(r+s+t) & = & r(s+t)\\ c(r+s+t) & = & s(r+t) \end{matrix}\right.\)
Definieer x = r + s
\(\left\{\begin{matrix} a(x+t) & = & xt\\ b(x+t) & = & r(s+t)\\ c(x+t) & = & s(r+t) \end{matrix}\right.\)
Uit de eerste vergelijking volgt: t = ax / (x-a).
Werk hiermee de t en s (= x - r) weg uit de 2e en 3e vergelijking:
\(\left\{\begin{matrix} bx+b\frac{ax}{x-a} & = & r(x - r +\frac{ax}{x-a})\\ cx+c\frac{ax}{x-a} & = & (x-r)(r+\frac{ax}{x-a}) \end{matrix}\right.\)
vermenigvuldig alles met (x-a):
\(\left\{\begin{matrix} bx(x-a)+abx & = & r((x - r)(x-a) +ax)\\ cx(x-a)+acx & = & (x-r)(r(x-a)+ax) \end{matrix}\right.\)
werk alle haakjes weg:
\(\left\{\begin{matrix} bx^2 & = & rx^2-r^2x-arx+ar^2+arx\\ cx^2 & = & rx^2 - arx +ax^2 -xr^2 +ar^2-arx \end{matrix}\right.\)
trek de eerste vergelijking af van de tweede vergelijking:
\((b-c)x^2 = 2arx - ax^2\)
x (= r + s) > 0 dus:
\((b-c)x = 2ar - ax\)
en
\(x = \frac{2ar}{a+b-c}\)
Substitueer dit resultaat in \(bx^2 = rx^2-r^2x+ar^2\), wat we weten uit het laatste stelsel hierboven.
Dit levert
\((b-r)(\frac{2ar}{a+b-c})^2 = ar^2-r^2\frac{2ar}{a+b-c}\)
deel alles door \(r^2\) en vermenigvuldig met \((a+b-c)^2\):
\((b-r)\cdot 4a^2 = a(a+b-c)^2-2ar(a+b-c)\)
en dit levert
\(r = \frac{(a+b-c)^2-4ab}{2(b-c-a)}\)
Uit r volgt de waarde van x:
\(x = \frac{2ar}{a+b-c}\)
vervolgens is
\(s = x-r\)
en
\(t = \frac{ax}{x-a}\)
Re: Stelsel oplossen met product van onbekenden
Geplaatst: 22 apr 2020, 12:37
door SafeX
Arie, bedankt voor je uitvoerige uitwerkingen. Heel wat werk! Ik moet ze nog nalopen.
Mij viel de cyclische verwisseling in de formules rechts op.
Stel dus:
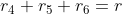
Dan volgt, als we de gegeven weerstanden in volgorde a, b en c noemen (opletten!):
=ar)
Dit is een kwadratische verg in r6, oplossen naar r, geeft:
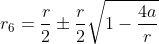
Evenzo:
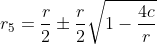
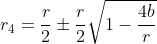
En nu komt de 'trick', want tellen we de drie verg op, wat moeten we dan uit de twee mogelijkheden kiezen.
Gegeven de getallen a, b en c, volgt r6 groter dan r/2 en r5 en r4 kleiner.
Zodat optellen geeft:
)
Rangschikken levert:
)
Delen door r/2, links en rechts:
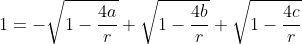
We hebben nu een verg in r, die we het best numeriek kunnen oplossen.
HP Prime geeft: r= 7170 en daarmee zijn r4, r5 en r6 eenvoudig uit te rekenen.