Wiskundeforum

Maar het klopt niet voor n = 2# = 2, 3# = 6, 5# = 30, 7# = 210.

de nieuwe ongelijkheid niet nee, maar de originele wel. het enige waar ik die nieuwe ongelijkheid, met p/(p-1) in het rechterlid voor nodig had was om te bewijzen dat de originele ongelijkheid klopte voor alle machten van alle priemgetallen.

Dat betekent dat als je een een getal hebt waarvoor de originele ongelijkheid klopt, dat je dan een aantal van de unieke priemfactoren van dat getal kan nemen en ze tot een macht heffen die zo hoog is als je wil. vb: originele vergelijking werkt voor 30(2*3*5), dus werkt hij ook voor elke 2^a*3^b*5^c. maar ook voor elke p>2*q>3*r>5. snap je?

Ah, snap ik. Je kan eens zoeken of het nieuwe resultaten zijn. Zo ja, kan je het publiceren.

ik ben nog aan het zoeken of iemand het al eerder heeft bedacht (tot nu toe niets), maar ik had twee vragen.
1. is dit echt zo belangrijk?
2. hoe publiceer je zoiets, airxiv?

Mastrem schreef: 1. is dit echt zo belangrijk?

Het gaat over een milleniumprobleem. Als het nieuw is, zou ik ervoor gaan.

Mastrem schreef: 2. hoe publiceer je zoiets, airxiv?

Ja, kan via arXiv.

oké, dan ga ik daar eens aan beginnen, ik ben voorlopig wel even bezig

ik heb een foutje in mijn bewijs gevonden, maar het vervolgens zodanig aangepast dat ik de ongelijkheid kan bewijzen voor alle oneven getallen, mits ik het volgende probleem kan oplossen:

wat zijn de restricties voor in termen van , zodat:



ik kom er niet uit, jij wel?

Je zou kunnen delen door a/(ax-1)) (voor noemer niet 0) aan beide kanten. Verder zou ik een matrix T maken waar het coördinaat T(a, x) aangeeft of de ongelijkheid klopt voor die waarden van a en x.

bedankt, dat helpt me alweer wat verder.

maar is er geen manier om twee functies f en g in termen van a te maken zodat als:

dat het dan klopt (wat ik wil weten of het werkt voor a=pn#/2 en ax=pn+1#/2).

Het enige wat ik kan bedenken is een matrix. *Misschien* geeft het een idee waar je moet zoeken en misschien kan je het vermoeden bewijzen.

okay, dan ga ik daar eens mee aan de gang.

door alleen halve primorials te gebruiken, heb ik de functie zover vereenvoudigt:

(ik kon geen # gebruiken voor primorials, vandaar die A's)

zou dit wel te bewijzen te zijn voor waarden van n groter dan een constante c?
we weten dat:
en:

ipv bovenstaande gigantische functies heb ik nu:



log is hier base e

valt dit te bewijzen?

volgens mij is het waar voor n>4, maar ik kan het niet bewijzen...

Na het inzetten van wat zwaarder geschut (Euler product / zeta functie) heb ik dit gekregen:

en dus:

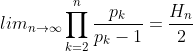
en dus kunnen we ongelijkheid voor n naar oneindig als volgt opschrijven:

en aangezien n naar oneindig gaat