Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Post hier al je algemene vragen over wiskunde in het voortgezetonderwijs /1ste graad ASO-TSO-BSO.
-
Xyrr
- Nieuw lid

- Berichten: 3
- Lid geworden op: 02 apr 2014, 02:06
Bericht
door Xyrr » 02 apr 2014, 02:18
Hallo allemaal,
Ik ben bezig door het boek van Craats heen te werken en loop bij onder andere 5.33e tegen niet zozeer een probleem maar wel een vraagstuk aan.
De opgave van 5.33e is om het volgende te ontbinden in factoren:
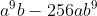
Het antwoord dat mij het meest praktische lijkt is
(a^{4}-16b^{4}))
Het boek komt echter met het antwoord
(a^{2}+4b^{2})(a+2b)(a-2b))
Beide antwoorden zijn correct, tenzij ik iets over het hoofd zie? Waarom verkiest men het tweede antwoord boven de eerste?
Thanks!
-
op=op
- Vergevorderde

- Berichten: 1087
- Lid geworden op: 23 apr 2010, 18:11
Bericht
door op=op » 02 apr 2014, 08:03
De bedoeling is altijd om zo ver mogelijk in factoren te ontbinden.
Als je b.v.
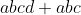
moet ontbinden, dan zou dat op heel veel manieren kunnen, b.v.
)
, maar er is maar één manier om het maximaal te ontbinden (
)
).
-
Xyrr
- Nieuw lid

- Berichten: 3
- Lid geworden op: 02 apr 2014, 02:06
Bericht
door Xyrr » 02 apr 2014, 14:31
Ik snap dat er inderdaad zoveel mogelijk buiten de haakjes moet worden geplaatst maar dat is mijn antwoord toch ook gebeurd? Het antwoord in het boek verschilt pas van de mijne bij de tweede
)
wat in het boek genoteerd wordt als
(a+2b)(a-2b))
Het resultaat is hetzelfde, maar waarom schrijft men het in langere vorm op? Ik vind het antwoord er persoonlijk in ieder geval niet duidelijker van worden.
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 02 apr 2014, 14:41
Xyrr schreef:Ik snap dat er inderdaad zoveel mogelijk buiten de haakjes moet worden geplaatst maar dat is mijn antwoord toch ook gebeurd? Het antwoord in het boek verschilt pas van de mijne bij de tweede
)
wat in het boek genoteerd wordt als
(a+2b)(a-2b))
Het resultaat is hetzelfde, maar waarom schrijft men het in langere vorm op? Ik vind het antwoord er persoonlijk in ieder geval niet duidelijker van worden.
Zie je dan geen verschil in
)
en
(a^{2}-b^{2}))
en
(a+2b)(a-2b))
...
-
David
- Moderator

- Berichten: 4927
- Lid geworden op: 14 mei 2009, 16:22
Bericht
door David » 03 apr 2014, 12:01
SafeX schreef:Zie je dan geen verschil in
)
en
(a^{2}-b^{2}))
en
(a+2b)(a-2b))
...
(Ja,
 = (a^{2}+4b^{2})(a^{2}-4b^{2}) \ne (a^{2}+4b^{2})(a^{2}-b^{2}))
)
Je kan nog zeggen dat je in zoveel mogelijk factoren wilt ontbinden.
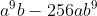
heeft een factor,
(a^{4}-16b^{4}))
heeft er drie
(a^{2}+4b^{2})(a+2b)(a-2b))
heeft er zes
Dus kies je
(a^{2}+4b^{2})(a+2b)(a-2b))
als antwoord.
(Verder gaan met ontbinden verandert het domein van a of b en dat is niet wat je wilt).
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 05 apr 2014, 20:25
David schreef:SafeX schreef:Zie je dan geen verschil in
)
en
(a^{2}-b^{2}))
en
(a+2b)(a-2b))
...
(Ja,
 = (a^{2}+4b^{2})(a^{2}-4b^{2}) \ne (a^{2}+4b^{2})(a^{2}-b^{2}))
)
Bedankt voor het aangeven van de fout ... , ik hoop dat de TS dit heeft doorzien.
Dus kies je
(a^{2}+4b^{2})(a+2b)(a-2b))
als antwoord.
(Verder gaan met ontbinden verandert het domein van a of b en dat is niet wat je wilt).
Wat bedoel je met de laatste opmerking ...
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Bericht
door arno » 06 apr 2014, 12:06
SafeX schreef:David schreef:Dus kies je
(a^{2}+4b^{2})(a+2b)(a-2b))
als antwoord.
(Verder gaan met ontbinden verandert het domein van a of b en dat is niet wat je wilt).
Wat bedoel je met de laatste opmerking ...
Wat David volgens mij bedoelt is dat
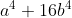
en
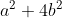
wel in de vorm (p-q)(p+q) te ontbinden is als je complexe getallen toelaat.
@David: Merk op dat
^2-8a^2b^2=(a^2-2ab\sqrt{2}+4b^2)(a^2+2ab\sqrt{2}+4b^2))
. Merk verder op dat a²-2ab√2+4b² = (a-b√2)²+2b² en dat a²+2ab√2+4b² = (a+b√2)²+2b², wat dus als uiteindelijke ontbinding
(a^2+2ab\sqrt{2}+4b^2)(a^{2}+4b^{2})(a+2b)(a-2b))
als antwoord oplevert. Zolang je als grondverzameling alleen reële getallen hebt is een verdere ontbinding van a²-2ab√2+4b² en a²+2ab√2+4b², en ook die van a²+4b², inderdaad niet mogelijk.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 06 apr 2014, 13:36
@arno
Als ik dat vraag aan iemand die reageert, dan ook graag antwoord van deze persoon ...
Houd ook rekening met de formules en vb die de TS op dit moment kent ...
-
Xyrr
- Nieuw lid

- Berichten: 3
- Lid geworden op: 02 apr 2014, 02:06
Bericht
door Xyrr » 08 apr 2014, 01:36
Thanks voor de hulp en excuus voor de late reactie. Ik heb de fout inderdaad doorzien en genoegen genomen met het feit dat men zo ver mogelijk dient te ontbinden. Nogmaals bedankt

-
David
- Moderator

- Berichten: 4927
- Lid geworden op: 14 mei 2009, 16:22
Bericht
door David » 08 apr 2014, 11:25
Mooi dat dit opgelost is.
Wat ik meer bedoelde is dat je a-b niet wilt ontbinden als
(\sqrt{a}+\sqrt{b}))
en nog verder maar dan mogen a of b niet negatief zijn.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
-
David
- Moderator

- Berichten: 4927
- Lid geworden op: 14 mei 2009, 16:22
Bericht
door David » 08 apr 2014, 14:28
arno schreef:Zolang je als grondverzameling alleen reële getallen hebt is een verdere ontbinding van a²-2ab√2+4b² en a²+2ab√2+4b², en ook die van a²+4b², inderdaad niet mogelijk.
Bedoel je 'gehele getallen' in plaats van 'reële getallen'?
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Bericht
door arno » 08 apr 2014, 17:15
David schreef:arno schreef:Zolang je als grondverzameling alleen reële getallen hebt is een verdere ontbinding van a²-2ab√2+4b² en a²+2ab√2+4b², en ook die van a²+4b², inderdaad niet mogelijk.
Bedoel je 'gehele getallen' in plaats van 'reële getallen'?
Nee, ik bedoel echt reële getallen. Bedenk dat a²-2ab√2+4b² = (a-b√2)²+2b² en dat a²+2ab√2+4b² = (a+b√2)²+2b², dus dat dit binnen de grondverzameling van de reële getallen niet verder te ontbinden is.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel



