Factoren buiten haakjes brengen
Re: Factoren buiten haakjes brengen
We zijn toch bezig met:
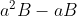
Re: Factoren buiten haakjes brengen
Ja. maar ik liet het antwoord of de uitwerking zien zoals het moet misschien dat, dat me nog verder kan helpen.
Re: Factoren buiten haakjes brengen
Maak dat nu eerst af, daarna zien we verder ...
Dus: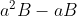
Dus:
Re: Factoren buiten haakjes brengen
Ja er zijn twee dezelfde factoren in de termen 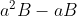 dat is a en b
dat is a en b
Re: Factoren buiten haakjes brengen
Dat zijn a en B (ik hoop dat je verschil ziet tussen b en B) ...
Haal die factoren buiten haakjes ...
Haal die factoren buiten haakjes ...
Re: Factoren buiten haakjes brengen
Ja ik zie het verschil tussen b en B. Ik heb het nu buiten haakjes gehaald aB(a+1)(-1)
Re: Factoren buiten haakjes brengen
Ik begrijp niet hoe je aan het onderstaande komt:
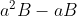
)
Wat blijft staan van de term a^2B en wat van de tweede term
Je hebt twee termen a^2B en -aB (bedenk dat een term een teken heeft!), als je zelfde factoren buiten haakjes haalt blijven binnen de haakjes dus weer twee termen over. Nu probeer je dat neg teken in orde te brengen met een factor -1 ...Soepkom schreef:aB(a+1)(-1)
Wat blijft staan van de term a^2B en wat van de tweede term
Re: Factoren buiten haakjes brengen
Niks blijft staan van de term a^2B en het wordt a(a-1)(b+1) dit snap ik nu omdat in de opgave a^2(b+1)-a(b+1) (b+1) gelijke factoren zijn dan blijft (a^2-a) nog over als a(a-1)
Re: Factoren buiten haakjes brengen
Meen je dat?Soepkom schreef:Niks blijft staan van de term a^2B ...
SafeX schreef:
Wat blijft staan van de term a^2B en wat van de tweede term
en als je nu B=b+1 terug invult ...
Vraag: heb je nu begrepen waarom we B hebben gekozen voor de factor b+1 ?
Re: Factoren buiten haakjes brengen
Vraag: heb je nu begrepen waarom we B hebben gekozen voor de factor b+1 ? nee
Wat blijft staan van de term a^2B en wat van de tweede term: a^2-a blijft staan want (b+1) is er al uit.
Wat blijft staan van de term a^2B en wat van de tweede term: a^2-a blijft staan want (b+1) is er al uit.
Re: Factoren buiten haakjes brengen
Heb je wel begrepen dat als je b+1 vervangt door B, je de volgende formule krijgt:Soepkom schreef:Vraag: heb je nu begrepen waarom we B hebben gekozen voor de factor b+1 ? nee
Zo ja, vind je deze formule overzichtelijker dan de opgave ...SafeX schreef: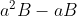
Re: Factoren buiten haakjes brengen
Heb je wel begrepen dat als je b+1 vervangt door B, je de volgende formule krijgt:
dit zie ik nu ja. Ja ik vindt de formule die jij hebt opgesteld overzichtelijker.
Re: Factoren buiten haakjes brengen
Mooi, kan je nu andere opgaven, van deze soort, ook maken ...
Opm: Ik heb je bericht aangepast, anders is het niet begrijpelijk
Opm: Ik heb je bericht aangepast, anders is het niet begrijpelijk
Re: Factoren buiten haakjes brengen
Er zijn nog een aantal opgaven waar ik niet uitkom, het zijn de volgende.
a.^2+(a+1))
b.^2+4(a+3))
c.^2(b+1)-2(a+3)(b+1))
d.^2(a+2)-(a-1)(a+2)^2)
e.^2(a-2)+9(a+2)(a-2)^2)
f.^3+6(a+4)^2(a+2))
De letters zijn er alleen om te kenmerken, met welke opgaven ik mee bezig ben.
Dit zijn mijn uitwerkingen.
a.^2+(a+1)=+1+a+1=(a+2)(a+1))
b.^2+4(a+3)=+2+4(a+3)=2(a+5)(a+3))
c.^2(b+1)-2(a+3)(b+1)=-2+a+3=(a+3)(b+1)(a+1))
d.^2(a+2)-(a-1)(a+2)^2=+a+2-a-1=(a-1)(a+2)(1))
e.^2(a-2)+9(a+2)(a-2)^2=+3+9+a-2+a+2=(a+2)(a-2)(12+2a))
f.^3+6(a+4)^2(a+2)=-2+a+4+6+a+2=(a+4)(a+4)(2a+10))
a.
b.
c.
d.
e.
f.
De letters zijn er alleen om te kenmerken, met welke opgaven ik mee bezig ben.
Dit zijn mijn uitwerkingen.
a.
b.
c.
d.
e.
f.

