Het eerste nulpunt is zo gevonden:
Daarmee is een deel van de oplossing bepaald, namelijk het interval
Echter is er nog een tweede deel:
Stel bv als x negatief, dan:

Wat is:sebuts schreef:Ergens ga ik waarschijnlijk de mist in met een tekenwisseling, maar zie het niet zo
sebuts schreef:
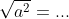
Ja, thanksDavid schreef:
Dus x-3 > 1/3 of x-3 > -1/3
Lukt het zo?
SafeX schreef: Wat is:
sebuts schreef:
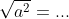
En als a<0 is ...sebuts schreef: a of meer specifiek:^{\frac{1}{2}} = a^{\frac{2}{2}} = a^1 = a)
Dat is toch hetzelfde, wantSafeX schreef:En als a<0 is ...sebuts schreef: a of meer specifiek:^{\frac{1}{2}} = a^{\frac{2}{2}} = a^1 = a)
Omdat er eigenlijk stondSafeX schreef: Opm: let op de aanpassing in je formule, waarom is dat nodig?
Stel a=-2 , dan staat er (nu):En als a<0 is ...sebuts schreef: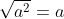
Dit begrijp ik niet: er stond als exponent 2 1/2 en dat is niet hetzelfde als 2*1/2 ...Omdat er eigenlijk stondSafeX schreef: Opm: let op de aanpassing in je formule, waarom is dat nodig?, volgorde van bewerking.