Ik kan nog wel een situatiebeschrijving geven; Eerst had ik de afstand berekend in km/h die hij had afgelegd op de lopende band.
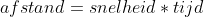
tijd=15/60 uur
snelheid= 9,8
9,8*(15/60)=2,45km
Dus de afstand die hij had afgelegd op de lopende band is gelijk aan 2,45 km
Het hellingsgetal van de helling van de lopende band was 0,7. Dus gebruikte ik de inverse tangens om de hellingshoek te achterhalen.
Daaruit kwam tan-1(0,7)=34,99...
Hierna had ik met cosinus de schuine zijde berekend (zie uitwerkingen)
cos(A)= AB/AC
cos(34,99...)=2,45/AC
AC= 2,45/ cos(34,99...)= 2,9...km
2,9...km= 2990,6...km
2990,6 m is het aantal meters dat die zou hebben gelopen als die echt op een berg liep.
Maar wat ik dus niet snap is wat ik simpelweg moest berekenen. De overstaande rechthoekszijde van hoek A of de schuine zijde AC


