Meestal vind ik de uitleg van Hofstede glashelder...
Hier geeft hij de volgende stellingen over kettingbreuken:
T(n) = a(n)• T(n-1) + T(n-2) en N(n) = a(n)• N(n-1) + N(n-2)
T is de teller, N is de noemer en a is een getal uit de kettingbreuk. Alles tussen haakjes moet een onderschrift zijn.
Vervolgens zegt hij: Als we deze rekenregel willen doorvoeren tot en met breuk nummer nul, dan moeten we T(0) en N(0) handig kiezen. Er moet dan namelijk gelden:
T(2) = a(2)• T(1) + T(0) = a(2)• a(1) + T(0) en ook N(2) = a(2)N(1) + N(0) = a(2)• 1 + N(0)
Daaruit volgt T(0) = 1 en N(0) = 0
Ik begrijp echter niet hoe je die T(0) = 1 hieruit onttrekt...
Ik heb dus: a(2) = N(2) ; a(1) = T(1) ; N(1) = 1 en N(0) = 0
Breuk nummer nul
Re: Breuk nummer nul
Een beetje vreemd:
doorgaans noteren we kettingbreuken in deze vorm:
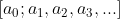
zie bijvoorbeeld https://nl.wikipedia.org/wiki/Kettingbreuk
De nulde convergent is dan
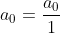
en dan is dus
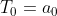
en
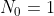
Zie https://nl.wikipedia.org/wiki/Kettingbreuk#Convergenten, waarbij ze daar de convergent als p/q schrijven in plaats van T/N:
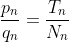
In deze notatie bereken jij dan waarschijnlijk convergent nummer -1, en dat zullen we nu doen:
Convergent nummer 1 is
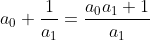
dus
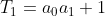
en
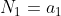
Met de recursieve formule kunnen we ook schrijven:
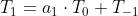
en
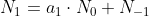
Vullen we hier nu de waarden van T[0], N[0], T[1] en N[1] in zoals we die hierboven vonden, dan krijgen we:
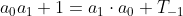
en
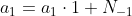
en hieruit kunnen we T[-1] en N[-1] oplossen:
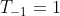
en
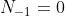
Kan het zijn dat dit bedoeld wordt?
doorgaans noteren we kettingbreuken in deze vorm:
zie bijvoorbeeld https://nl.wikipedia.org/wiki/Kettingbreuk
De nulde convergent is dan
en dan is dus
en
Zie https://nl.wikipedia.org/wiki/Kettingbreuk#Convergenten, waarbij ze daar de convergent als p/q schrijven in plaats van T/N:
In deze notatie bereken jij dan waarschijnlijk convergent nummer -1, en dat zullen we nu doen:
Convergent nummer 1 is
dus
en
Met de recursieve formule kunnen we ook schrijven:
en
Vullen we hier nu de waarden van T[0], N[0], T[1] en N[1] in zoals we die hierboven vonden, dan krijgen we:
en
en hieruit kunnen we T[-1] en N[-1] oplossen:
en
Kan het zijn dat dit bedoeld wordt?
-
stijn.boshoven
- Vast lid

- Berichten: 26
- Lid geworden op: 30 jul 2017, 15:32
Re: Breuk nummer nul
Aha!
T(1) = a(1) a(0) + 1
Die miste ik dus...
Ontzettend bedankt!
Hofstede noemt dus die a(0) waar jij het over hebt de a(1)...
http://www.hhofstede.nl/modules/kettingbreuken.htm
T(1) = a(1) a(0) + 1
Die miste ik dus...
Ontzettend bedankt!
Hofstede noemt dus die a(0) waar jij het over hebt de a(1)...
http://www.hhofstede.nl/modules/kettingbreuken.htm
