Merk op dat √a uitsluitend gedefinieerd is voor a≥0, dus er geldt in ieder geval dat 2x+1≥0, dus x≥-½. Merk verder op dat |a| = a voor a≥0, dus er geldt dat |x+1| = x+1 voor x≥-1. Vanwege het feit dat x≥-½ betekent dit dus dat moet gelden dat
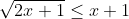
. Los nu eens de wortelvergelijking
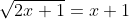
op en bedenk dat in ieder geval moet gelden dat x≥-½. Wat volgt daaruit voor de oplossing van de ongelijkheid?
Een polynoom van graad n heeft de algemene gedaante
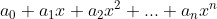
, waarbij
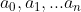
coëfficiënten zijn die uit een gegeven getalverzameling, zoals de gehele, rationale, reële of complexe getallen, kunnen worden gekozen. Stel f(x) is een polynoom van graad n en g(x) is een polynoom van graad m met m≤1≤n, dan zijn er 2 uniek bepaalde polynomen q(x) en r(x) te vinden met graad(r(x))<graad(g(x)) waarvoor geldt dat f(x) = q(x)·g(x)+r(x), waarbij q(x) het quotiëntpolynoom en r(x) het restpolynoom bij deling van f(x) door g(x) voorstelt. Indien g(x) = x-a geldt dat r(x) = f(a). Dit is de zogenaamde reststelling voor polynomen. Voor r(x) = 0 betekent dit dat x-a een factor van f(x) is en dat x = a dan een nulpunt van f(x) is. Dit is de zogenaamde factorstelling voor polynomen.
Om bij een polynoom van graad n met geheeltallige coëfficiënten de nulpunten te vinden bepaal je alle mogelijke delers van de hoogste coëfficiënt, dus van
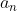
. Stel dat a zo'n deler is waarvoor geldt dat f(a) = 0, dan is x = a dus een nulpunt van f(x) en is x-a een factor van f(x).
Bij het voorbeeld in je boek is gegeven dat q(x) = x-1, dus dat f(x) = (x-1)g(x)+r(x). Bepaal nu aan de hand van de gegeven uitdrukking voor f(x) eens de uitdrukking voor g(x) en r(x).
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
. Ik heb één korte vraag en één lange vraag. 
