Indien je het met combinaties op wilt lossen:
Eerste helft:
In de eerste helft waren er 3 doelpunten waaruit A er 2 moet kiezen:
dat geeft 3 nCr 2 = 3 mogelijkheden.
Noot: doorgaans geven we de voorkeur aan deze notatie:
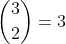
(dit is de gebruikelijke notatie, nCr is de afkorting hiervoor op je rekenmachine, sommige docenten willen niet dat je nCr gebruikt)
Merk op dat als de doelpunten van A gekozen zijn, B het overgebleven doelpunt maakt.
Je kan ook het ene doelpunt van B uit de 3 mogelijkheden kiezen, hiervoor zijn er
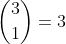
mogelijkheden.
Je ziet dat daar hetzelfde uitkomt.
Het aantal mogelijkheden voor de eerste helft had je zelf ook al gevonden.
Tweede helft:
In de tweede helft zijn er 6 doelpunten gescoord: A 2 en B 4
(je schreef A 4, maar dat is de eindstand, mogelijk een schrijffout).
Er zijn 6 nCr 2 = 15 manieren om de 2 doelpunten van A uit die 6 te kiezen, de overige 4 zijn voor B.
(of: er zijn 6 nCr 4 = 15 manieren om de 4 doelpunten van B uit die 6 te kiezen, de overige 2 zijn voor A.)
Totale wedstrijd:
Er zijn 3 verschillende mogelijke spelverlopen voor de eerste helft
EN
er zijn 15 verschillende mogelijke spelverlopen voor de tweede helft
Voor elk van de 3 spelverlopen van de eerste helft hebben we 15 mogelijke spelverlopen voor de tweede helft.
Hoeveel mogelijke spelverlopen hebben we dan in totaal?
(zie je nu of we moeten optellen of moeten vermenigvuldigen?)
(vergelijk dit zo nodig met een afvaardiging van 1 jongen EN 1 meisje uit een klas met
10 jongens en 12 meisjes, hoeveel afvaardigingen zijn er mogelijk?)