Ik weet niet zeker of ik deze vraag in de goede rubriek heb gezet, maar goed. Mijn vraag is het volgende.
Ik probeer het aantal priemgetallen zeer nauwkeurig te bepalen, nu kom ik deze formule vaak tegen op internet:
Hierbij is log geloof ik de natuurlijke logaritme.
en ik weet ook dat
En nu staat er voor de tweede term het volgende:
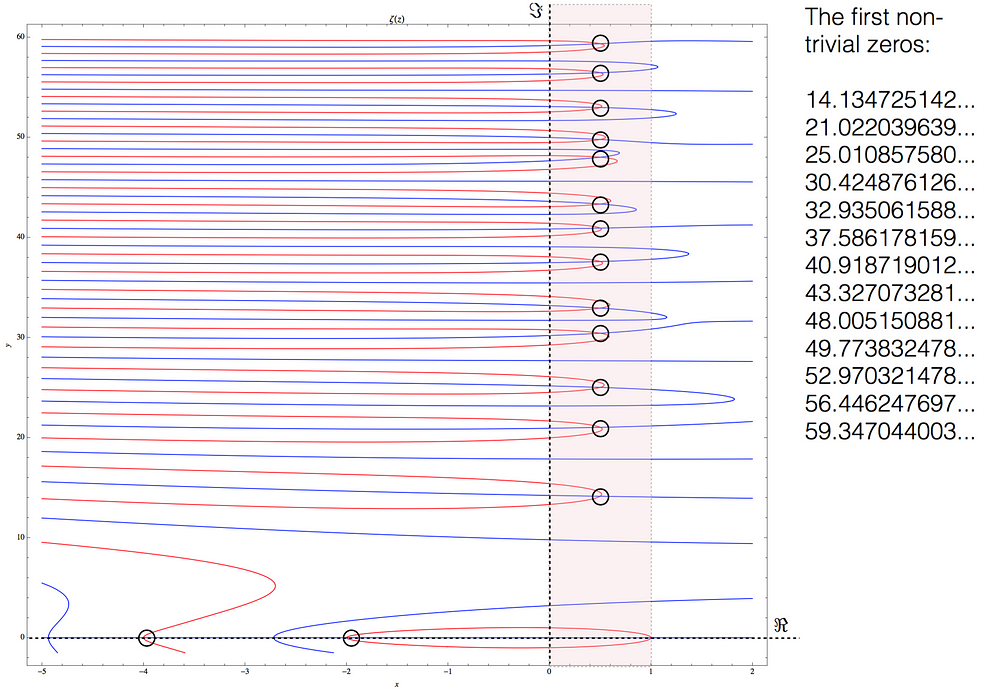
The second term, or “periodic term” is the sum of the logarithmic integral of x to the power ρ, summed over ρ, which are the non-trivial zeros of the Riemann zeta function. It is the term that adjusts the overestimate of the principle term.
Wat zijn de non triviale nullen van de riemann zeta functie ? Ik probeer overal op internet een voorbeeld uitwerking van deze formule te vinden maar die vind ik niet.
En voor de vierde staat het volgende:
The fourth and final term is an integral which is zero for x < 2 because there are no primes smaller than 2. It has its maximum value at 2, when its integral equals approximately 0.1400101….
En wat is t bij de 4de term ?
Uw hulp zal erg gewaardeerd worden. Bij voorbaat dank.