Goedendag,
Voor een sterkteleeropgave heb ik de formule: sigma = (M·c)/I.
Als ik c wil weten dan doe ik: c = (sigma·I)/M. Hieruit volgt c = (sigma/M)·I.
Vanuit de sterkteleer weet ik dat I = 1/4·pi·(R^4-r^4)
Aangezien R=c wordt het dan: I = 1/4·pi·(c^4-r^4).
Als ik de twee formules samenvoeg krijg ik: c=(sigma/M)·1/4·pi·(c^4-r^4).
Als ik de alle c's naar links breng krijg ik: c/(c^4-r^4) = (sigma/M)·1/4·pi.
Hoe haal ik c eruit?
Met vriendelijke groet,
Bob Wittebrood
Ombouwen formule (3)
Re: Ombouwen formule (3)
Kan je ook aangeven wat de letters betekenen en hun dimensie?
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Ombouwen formule (3)
Je weet dat 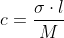 en dat
en dat ) , dus invullen van de tweede formule in de eerste geeft de gevraagde uitdrukking voor c.
, dus invullen van de tweede formule in de eerste geeft de gevraagde uitdrukking voor c.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Ombouwen formule (3)
@ SafeX: C= uiterste vezelafstand (diameter) [mm]; I= traagheidsmoment [mm^4]; M= Buigmoment [Nmm]; R= straal buitendiameter [mm]; r= staal binnendiameter [mm].
@ arno: Van de waarde R weet ik dat deze gelijk is aan c. Als ik c invul voor R in de rechter formule dan heb ik aan beide kanten een c. Doordat de rechterzijde c^4 is loop ik vast. Ik heb beide c's al aan de linkerzijde gebracht. Hoe haal ik c eruit?
@ arno: Van de waarde R weet ik dat deze gelijk is aan c. Als ik c invul voor R in de rechter formule dan heb ik aan beide kanten een c. Doordat de rechterzijde c^4 is loop ik vast. Ik heb beide c's al aan de linkerzijde gebracht. Hoe haal ik c eruit?
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Ombouwen formule (3)
Er geldt dus als ik goed begrijp dat ) , wat te herloeiden is tot
, wat te herloeiden is tot 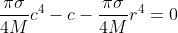 . Dit is een vierdegraadsvergelijking in c die je het beste numeriek kunt oplossen. Als je bekend bent met differentiëren zou je de methode van Newton-Raphson toe kunnen passen, en anders zou je de methode regula falsi toe kunnen passen. Een vierdegraadsvergelijking is weliswaar exact op te lossen, maar de vorm waarin deze oplossing verschijnt is algebraïsch nogal ingewikkeld. Het is dus vanuit practisch oogpunt handiger om een numerieke methode toe te passen.
. Dit is een vierdegraadsvergelijking in c die je het beste numeriek kunt oplossen. Als je bekend bent met differentiëren zou je de methode van Newton-Raphson toe kunnen passen, en anders zou je de methode regula falsi toe kunnen passen. Een vierdegraadsvergelijking is weliswaar exact op te lossen, maar de vorm waarin deze oplossing verschijnt is algebraïsch nogal ingewikkeld. Het is dus vanuit practisch oogpunt handiger om een numerieke methode toe te passen.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Ombouwen formule (3)
Ik kan je redenatie volgen en ik heb even gegoogeld naar de methode van Newton-Raphson en ik snap de bedoeling ervan. Ik heb echter voor een andere numerieke methode gekozen waarbij ik de formule in Excel heb gezet om sneller de variabelen te kunnen doorrekenen t.o.v. de rekenmachine. Door de waarde c handmatig te corrigeren ben ik steeds dichter bij het antwoord gekomen. Ik ben geëindigd bij een getal met 3 cijfers achter de komma (c = 50,559 [mm]) waarmee de diameter D die ik zocht op afgerond 101,12 [mm] uit komt. Wel veel werk maar het doel heiligt de middelen.
Bedankt beide voor de hulp.
Bedankt beide voor de hulp.

