yoe
deze vergelijking kregen we op een test en ik krijg ze niet opgelost
(ab)log x =( (a)logx . (b)logx ) / ( (a)logx + (b)log x )
de getallen tussen haakjes zijn superscript, de grondtallen dus, het . is maal
alvast bedankt
logaritme vergelijking
-
Sjoerd Job
- Vergevorderde

- Berichten: 1144
- Lid geworden op: 21 jan 2006, 15:09
- Locatie: Krimpen aan den IJssel
Re: logaritme vergelijking
Ok, even simpeler...miboe schreef:yoe
deze vergelijking kregen we op een test en ik krijg ze niet opgelost
(ab)log x =( (a)logx . (b)logx ) / ( (a)logx + (b)log x )
de getallen tussen haakjes zijn superscript, de grondtallen dus, het . is maal
alvast bedankt
Ok... Dus nu moeten we dit oplossen?
Even simpeler! Gekke logarithmes! Ik wil het bij LN houden
Dit staat natuurlijk gelijk aan
Na nog een stap komen we op
ln(x) buiten haakjes halen
ln(a)+ln(b) = ln(ab)... (feit, rekenregel)
Dus, dan komen we bij hetzelfde uit, en het kan niet anders, of deze formule klopt altijd!
``Life is complex. It has real and imaginary parts.''
Het kan korter!
Gebruik de algemene formule: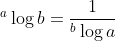 , mits a en b aan de voorwaarden van het grondtal voldoen.
, mits a en b aan de voorwaarden van het grondtal voldoen.
(bewijs deze formule zelf met de laatste rekenregel)
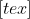 ^{ab}\log{x}=\frac{^a\log{x}\times^b\log{x}}{^a\log{x}+^b\log{x}}
^{ab}\log{x}=\frac{^a\log{x}\times^b\log{x}}{^a\log{x}+^b\log{x}}
Het linkerlid schrijven we: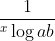 (LR)
(LR)
Het rechterlid wordt: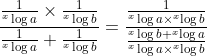 ,
,
nu vereenvoudigen tot door teller en noemer te vermenigvuldigen met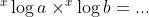
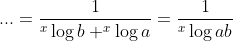 en dit is (LR).
en dit is (LR).
Gebruik de algemene formule:
(bewijs deze formule zelf met de laatste rekenregel)
Het linkerlid schrijven we:
Het rechterlid wordt:
nu vereenvoudigen tot door teller en noemer te vermenigvuldigen met

