Iemand stelde mij een keer deze vraag, en ik kwam er ook niet echt uit. Maar ik wil toch heel erg graag weten hoe je dit nou moet uitrekennen. Alvast bedank als jullie mij kunnen helpen.
Er zijn 20000 ballen, elke bal heeft een andere kleur. Je pakt aselect 300 ballen, met terug leggen. Dus je pakt een bal, noteert de kleur en legt deze terug. Hoe groot is de kans, dat je twee keer dezelfde knikker pakt.
Alvast bedankt,
Stijn
Ballen pakken
-
Sjoerd Job
- Vergevorderde

- Berichten: 1144
- Lid geworden op: 21 jan 2006, 15:09
- Locatie: Krimpen aan den IJssel
Afgezien van de opmerking van SafeX...
De kans dat iets gebeurt: = \frac{A}{U}) Het aantal gunstige mogelijkheden door het aantal mogelijkheden.
Het aantal gunstige mogelijkheden door het aantal mogelijkheden.
Op hoeveel manieren kunnen wij 300 knikkers pakken? 2000^300 (erg groot).
Ik interpreteer deze vraag als "2 of meer" dezelfden.
 = P(U) - P(NIET A) = 1 - P(NIET A))
P(NIET A) = allemaal verschillende = 2000! / 1700!
Uitrekenen, en dan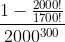 uitrekenen, en je hebt je kans
uitrekenen, en je hebt je kans 
Dacht ik, ik hoop dat het klopt.
De kans dat iets gebeurt:
Op hoeveel manieren kunnen wij 300 knikkers pakken? 2000^300 (erg groot).
Ik interpreteer deze vraag als "2 of meer" dezelfden.
P(NIET A) = allemaal verschillende = 2000! / 1700!
Uitrekenen, en dan
Dacht ik, ik hoop dat het klopt.
``Life is complex. It has real and imaginary parts.''
Je moet het als volgt berekenen:
Je hebt te maken met een binomiale kansverdeling
De formule is
P(k=0)=(300 0)*(1/20000)^0*(1-1/20000)^300=0.98511
P(k=1)=(300 1)*(1/20000)^1*(1-1/20000)^299=0.00004925
P(k=2)=(300 2)*(1/20000)^2*(1-1/20000)^298=0.000000000246
totaal=0.98511+0.00004925+0.000000000246=0.98516
Dus de kans dat je kleiner of gelijk aan 2 dezeelfde hebt is 98,516%
Je hebt te maken met een binomiale kansverdeling
De formule is
P(k=0)=(300 0)*(1/20000)^0*(1-1/20000)^300=0.98511
P(k=1)=(300 1)*(1/20000)^1*(1-1/20000)^299=0.00004925
P(k=2)=(300 2)*(1/20000)^2*(1-1/20000)^298=0.000000000246
totaal=0.98511+0.00004925+0.000000000246=0.98516
Dus de kans dat je kleiner of gelijk aan 2 dezeelfde hebt is 98,516%

