Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Post hier al je algemene vragen over wiskunde in het voortgezetonderwijs /1ste graad ASO-TSO-BSO.
-
zeebas
- Nieuw lid

- Berichten: 3
- Lid geworden op: 16 jan 2019, 16:04
Bericht
door zeebas » 16 jan 2019, 16:16
Beste Wiskundige, Hier een lastige vraag
 = (2\pi) / sin(2 \pi x) )
[0 < x < 1/2]
De Primitieve die hier bij hoort is gegeven:
 = Ln(tan(2 \pi x)))
De lijn
 / 3 )
Er is een vlakdeel A wat ingesloten wordt door de lijn en de f(x)
bereken deze oppervlakte exact
-
arie
- Moderator

- Berichten: 3917
- Lid geworden op: 09 mei 2008, 09:19
Bericht
door arie » 16 jan 2019, 19:30
Wat zijn de x-coördinaten van de snijpunten van de lijn met de grafiek in het gegeven interval \(\langle0, \frac{1}{2}\rangle\) ?
PS: ik heb de lay-out van je vraag iets aangepast: geneste FORMULE en LATEX haken werken niet...
-
zeebas
- Nieuw lid

- Berichten: 3
- Lid geworden op: 16 jan 2019, 16:04
Bericht
door zeebas » 16 jan 2019, 19:40
Dank, ik had dit nog niet eerder gebruikt.
De snijpunten waar ik op uit kom zijn
x= 1/6 of x = 1/3
-
arie
- Moderator

- Berichten: 3917
- Lid geworden op: 09 mei 2008, 09:19
Bericht
door arie » 16 jan 2019, 20:41
Klopt.
Maak een grove schets van de situatie, en je ziet dat we het oppervlak van A kunnen berekenen via:
\(\text{Opp}(A) = \left| \int_{1/6}^{1/3} \frac{4}{3}\pi \sqrt{3} \;dx - \int_{1/6}^{1/3} \frac{2\pi}{\sin(2\pi x)}\;dx\right|\)
of eenvoudiger:
\(\text{Opp}(A) = \left(\frac{1}{3} - \frac{1}{6}\right) \cdot \frac{4}{3}\pi \sqrt{3} - \int_{1/6}^{1/3} \frac{2\pi}{\sin(2\pi x)}\;dx\)
Kom je nu verder?
-
zeebas
- Nieuw lid

- Berichten: 3
- Lid geworden op: 16 jan 2019, 16:04
Bericht
door zeebas » 16 jan 2019, 21:41
Ik antwoord via mijn telefoon:
Als ik 1/3 invul in de primitieve krijg ik:
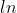
(
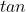
( 2Pi/3))
Tan van 2/3 pi = - Wortel 3
Ln( - Wortel 3 ) is niet mogelijk...
Dat is eigelijk waar ik vast loop
-
arie
- Moderator

- Berichten: 3917
- Lid geworden op: 09 mei 2008, 09:19
Bericht
door arie » 16 jan 2019, 22:13
De gegeven primitieve klopt niet, deze moet zijn:
\(\text{F}(x) = \ln(\tan(\pi \cdot x))\)
Hiermee zou het wel moeten gaan lukken.
PS: Ter controle:
\(\frac{d}{dx} \text{F}(x) = \frac{1}{\tan(\pi x)} \cdot \frac{1}{\cos^2(\pi x)}\cdot \pi = \frac{\pi}{\sin(\pi x) \cos(\pi x)}\)
\(= \frac{\pi}{\frac{1}{2}\sin(2\pi x)} = \frac{2\pi }{\sin(2\pi x)}\)