Er zijn 23 resultaten gevonden
- 27 feb 2024, 21:21
- Forum: Wiskundige puzzels
- Onderwerp: Hoeveel water in het blikje?
- Reacties: 16
- Weergaves: 6117
Re: Hoeveel water in het blikje?
Toen ik in het vorige probleem vastliep, was dat omdat er "iets naar nul liep" waar dat niet mocht. Deze keer vermoed ik dat er "iets naar oneindig loopt" waar dat niet mag... https://i.postimg.cc/pLMYqzy7/infinite.jpg Is dat inderdaad het probleem? En zo ja: graag een hint naar hoe ik dat oplos...
- 26 feb 2024, 21:39
- Forum: De Wiskundelounge
- Onderwerp: Het Grote Moppentrommeltopic
- Reacties: 48
- Weergaves: 101900
- 25 feb 2024, 15:27
- Forum: Tutorials en Minicursussen
- Onderwerp: 1300 wiskunde formules
- Reacties: 0
- Weergaves: 8418
1300 wiskunde formules
Gratis PDF met 1300 wiskunde formules.
https://www.e-kitabi.com/1300-math-form ... -for-free/
Even wachten tot de teller (net boven comments) op 0 staat, en je kan de download (9,3 MB) starten.

https://www.e-kitabi.com/1300-math-form ... -for-free/
Even wachten tot de teller (net boven comments) op 0 staat, en je kan de download (9,3 MB) starten.

- 25 feb 2024, 12:36
- Forum: Wiskundige puzzels
- Onderwerp: Hoeveel water in het blikje?
- Reacties: 16
- Weergaves: 6117
- 24 feb 2024, 17:32
- Forum: Wiskundige puzzels
- Onderwerp: Hoeveel water in het blikje?
- Reacties: 16
- Weergaves: 6117
Re: Hoeveel water in het blikje?
Nog even dit:
https://nl.wikipedia.org/wiki/Lijst_van_integralen
Hier is er nog één die wat uitgebreider is:arie schreef: ↑22 feb 2024, 11:44... lijsten met veel voorkomende integralen, zoals
https://en.wikipedia.org/wiki/Lists_of_integrals
https://nl.wikipedia.org/wiki/Lijst_van_integralen
- 24 feb 2024, 17:18
- Forum: Wiskundige puzzels
- Onderwerp: Hoeveel water in het blikje?
- Reacties: 16
- Weergaves: 6117
Re: Hoeveel water in het blikje?
Bedankt arie, voor weer een prachtige uitleg! Ik wil dit nieuwe vraagstuk ' from scratch ' oplossen. Dus vertrekkende van enkel de vergelijkingen voor kegel K en vlak V. Ik heb daarvoor jou afbeelding gepikt, en er een paar aanpassingen in aangebracht... https://i.postimg.cc/2SWCf79R/kegelvlak.jpg G...
- 14 feb 2024, 18:09
- Forum: Wiskundige puzzels
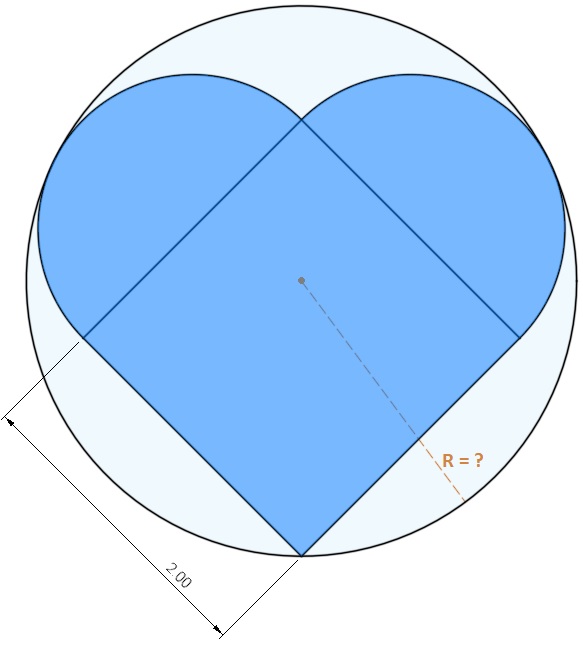
- Onderwerp: Eentje voor Valentijn ;-)
- Reacties: 0
- Weergaves: 4305
- 13 feb 2024, 21:50
- Forum: De Wiskundelounge
- Onderwerp: Optische illusies
- Reacties: 3
- Weergaves: 4497
Optische illusies
Ik ben ervan overtuigd dat wiskundigen 'van nature' ook fan zijn van optische illusies. Hoe dat komt kan ik niet zo onmiddellijk verklaren, maar... by all means ... spreek mij tegen... :wink: De klassiekers zullen jullie wel kennen, maar zopas kwam ik op Facebook een nieuwe tegen: https://i.postimg....
- 13 feb 2024, 19:56
- Forum: De Wiskundelounge
- Onderwerp: Het Grote Moppentrommeltopic
- Reacties: 48
- Weergaves: 101900
- 13 feb 2024, 15:42
- Forum: Wiskundige puzzels
- Onderwerp: Hoeveel water in het blikje?
- Reacties: 16
- Weergaves: 6117
Re: Hoeveel water in het blikje?
Kom je er zo uit? Nou... en of! :D Het volume van de (kwart)kegel in bovenstaand voorbeeld is: V=\int_{x=0}^{9}\int_{y=0}^{r}\sqrt{r^{2}-y^{2}}\;dy\;dx waarbij: r=\frac{x}{3} Stel: y=r\;\sin(u) dan: dy=r\;\cos(u)\;du en de grenzen: y=0 wordt u=0 y=r wordt u=\pi/2 We krijgen nu: \begin{equation} \be...
- 12 feb 2024, 17:04
- Forum: Wiskundige puzzels
- Onderwerp: Hoeveel water in het blikje?
- Reacties: 16
- Weergaves: 6117
Re: Hoeveel water in het blikje?
Dit blijkt toch een stuk moeilijker te zijn dan ik gedacht (lees: gehoopt) had... Hieronder een voorbeeld, en een plaatje van hoe ik het wou aanpakken: https://i.postimg.cc/vZ9mvcpg/kegel.jpg https://i.postimg.cc/tCPCN0HB/solver.jpg Zoals je ziet: ook mijn solver raakt er niet uit... Daarom een eers...
- 03 feb 2024, 12:07
- Forum: Wiskundige puzzels
- Onderwerp: Hoeveel water in het blikje?
- Reacties: 16
- Weergaves: 6117
Re: Hoeveel water in het blikje?
De berekening voor de piramide ging vrij makkelijk. Het viel mij op dat de waarden voor x, y en z de hele tijd 'goed zichtbaar' bleven, wat mij op een krankzinnig idee bracht: zou ik dit ook parametrisch kunnen oplossen? En ook dat was vrij makkelijk. :D Ik wil nu nog één stapje verder gaan, en het ...
- 01 feb 2024, 14:43
- Forum: Wiskundige puzzels
- Onderwerp: Hoeveel water in het blikje?
- Reacties: 16
- Weergaves: 6117
Re: Hoeveel water in het blikje?
Om mijn begrip van bovenstaande theorie te testen, wil ik het volume van een piramide berekenen. Ik plaats daarvoor een piramide (met ruitvormig grondvlak) op het XY-vlak, die ik dan 'vierendeel'. https://i.postimg.cc/cHJXM35d/piramide.jpg (Ja, ik weet het... V=\frac{\frac{8\;\cdot \;6}{2}\cdot 15}{...
- 27 jan 2024, 22:14
- Forum: Wiskundige puzzels
- Onderwerp: Hoeveel water in het blikje?
- Reacties: 16
- Weergaves: 6117
Re: Hoeveel water in het blikje?
Ik denk dat ik het helemaal begrijp. Of... toch voldoende om aan de slag te gaan met wat variaties. Weet je nog? Het 'kleine extra stukje' uit mijn start-post in dit topic? Wel... dat heb ik nu ook kunnen berekenen. :D ... die we met geschikte substituties kunnen oplossen. (integraal van som = som v...
- 26 jan 2024, 20:58
- Forum: Wiskundige puzzels
- Onderwerp: Hoeveel water in het blikje?
- Reacties: 16
- Weergaves: 6117
Re: Hoeveel water in het blikje?
Dit ga ik toch een paar keer stevig moeten herkauwen... 
Alvast erg bedankt voor de uitgebreide uitleg!
Alvast erg bedankt voor de uitgebreide uitleg!