Wiskundeforum

Ik zit weer vast met een vergelijking, namelijk deze:
sqrt(1+sqrt(x^4 -x²))=x-1
dit wordt
1+sqrt(x^4 -x²))=x²-2x+1
=>sqrt(x^4 -x²))=x(x-2)
=>x^4-x²=x²(x²-4x+4)
=>4x^3-5x²=0
=>x²(4x-5)=0

=>x=0 of x=5/4

de oplossing zegt dat er geen oplossingen in R zijn

Heb je je waarden ingevuld in de oorspronkelijke vergelijking?
Kan je verklaren wat je vind?

de ingevulde waarden geven
0=-1
en
1.391941091...=0.25

ik weet geen verklaring daarom dat ik het op dit forum heb gezet

Stef schreef:de ingevulde waarden geven
0=-1
en
1.391941091...=0.25

Je kan dat beter niet zo op je toets zetten;
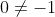
en

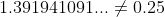
Stel even:
en
Je vond:
x=0 v x=5/4.
Nu:
Zo heb je neem ik aan dat uitgerekend. Het gaat me dan even over de notatie.

Dit is je vergelijking:

Je deed: kwadrateer
(trek 1 af)
(kwadrateer)


etcetera.

Omdat er een aantal keer gekwadateerd wordt, kunnen meerdere snijpunten ontstaan.
Ander voorbeeld buiten de opgave:
-x=x
Nu is er een oplossing; x=0. Kwadrateer beiden:
(-x)^2=(-1)^2*x^2=1*x^2=x^2
(x)^2=x^2

Opeens zijn alle x geldig.

Daarom is het nuttig om je gevonden waarden te controleren in de oorspronkelijke vergelijking. Dan kan je sowieso zien of je goed zit; als het dan niet klopt, kan je berekening ook nog onjuist zijn.

Het was dus niet juist :p

en zo zou ik het ook niet op een examen of zo schrijven hoor
ik werk normaal gewoon uit en als uitkomst heb ik dan
x=... V x=...

maar waar zit mijn fout nu?
Er is geen oplossing in R

Je moet op het eind je antwoord contoleren. Houd je daar, zeker bij wortelfuncties maar aan vast.
Je berekeningen zijn verder juist, maar geven soms meer waarden voor x dan er in werkelijkheid zijn.