Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Continue & discrete verdelingen, toevalsveranderlijken, betrouwbaarheidsintervallen, correlaties.
-
Thomas
- Gevorderde

- Berichten: 120
- Lid geworden op: 06 apr 2007, 02:02
Bericht
door Thomas » 24 okt 2007, 14:43
Stel, je hebt een spel waarbij de kans op winnen 0,27 is. Wanneer je niet wint, 0,73 kans, speel je nog een keer.
Wat is nu de kans op winnen bij twee pogingen?
Is het:
 \cdot 0,27)
of moet het voor twee pogingen:
 \cdot 0,27 + 0,27^2)
zijn?
Het gaat er wel om dat je na één keer winnen stopt.
Laatst gewijzigd door
Thomas op 04 nov 2007, 00:23, 1 keer totaal gewijzigd.
-
Thomas
- Gevorderde

- Berichten: 120
- Lid geworden op: 06 apr 2007, 02:02
Bericht
door Thomas » 24 okt 2007, 20:52
Als het een beetje vaag is graag even melden, dan probeer ik het anders uit te leggen.
-
Zwink
Bericht
door Zwink » 01 nov 2007, 11:57
Als je een winstkans hebt van 0,27% en dus een verlies kans van 0,73%, dan is de winstkans bij de 2e poging:
0,73*0,27
Een winstkans bij de 3e periode zou zijn:
0,73^2*0,27
Etcetera
-
Thomas
- Gevorderde

- Berichten: 120
- Lid geworden op: 06 apr 2007, 02:02
Bericht
door Thomas » 05 nov 2007, 13:17
Yup weet ik, maar ik ben op zoek naar de kans op slagen bij

pogingen waarbij je stopt nadat je succes hebt.
Stel je doet
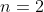
pogingen dan geldt:
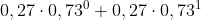
of moet ik er ook
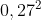
bij optellen?
-
luijs
- Vergevorderde

- Berichten: 347
- Lid geworden op: 18 aug 2006, 09:45
- Locatie: Tilburg
Bericht
door luijs » 05 nov 2007, 20:16
Is het dan niet gewoon de kans uitrekenen dat je NIET wint in

keer?
Edit: en dan uiteraard 1-die_kans
Ik ben het er niet mee eens!!
Of wel..?
-
Thomas
- Gevorderde

- Berichten: 120
- Lid geworden op: 06 apr 2007, 02:02
Bericht
door Thomas » 05 nov 2007, 22:35
Maakt het uit dan? Leg me even uit hoe dat dan ook al weer moet =)
Ik ben nooit een ster geweest in kansrekenen. Maar als jouw manier hetzelfde antwoord geeft als mijn manier voor verschillende waardes van

dan vind ik het goed!
-
Jerre
- Nieuw lid

- Berichten: 1
- Lid geworden op: 10 nov 2007, 00:00
Bericht
door Jerre » 10 nov 2007, 00:07
hey
als ik het goed begrijp:
je hebt de kans op succes (p): 0,27
je hebt de kans op mislukken (q): 0,73
en dit is een 'proef' die je n keer moet herhalen?
Typevoorbeeld van een binomiale kansverdeling
Formule:
P(x=k) = (Combinatie van k uit n) * p^k*q^(n-k)
=> kans op k keer succes
formule voor combinatie van k uit n:
n!/((n-k)!*k!)
Hopelijk heb je er wat aan
-
Thomas
- Gevorderde

- Berichten: 120
- Lid geworden op: 06 apr 2007, 02:02
Bericht
door Thomas » 10 nov 2007, 04:32
Jerre schreef:hey
als ik het goed begrijp:
je hebt de kans op succes (p): 0,27
je hebt de kans op mislukken (q): 0,73
en dit is een 'proef' die je n keer moet herhalen?
Typevoorbeeld van een binomiale kansverdeling
Formule:
P(x=k) = (Combinatie van k uit n) * p^k*q^(n-k)
=> kans op k keer succes
formule voor combinatie van k uit n:
n!/((n-k)!*k!)
Hopelijk heb je er wat aan
Eerlijk gezegd niet volgens mij. Want bij mij gaat het er om dat je na één succes stopt met proberen. Bij drie pogingen zijn de mogelijkheden op één keer slagen en twee keer falen:
S
F S
F F S
Zou je doorgaan ook na het succes dan zou het dit zijn:
S F F
F S F
F F S
Hoe zit het met die kansen?
-
Hugo
- Vergevorderde

- Berichten: 926
- Lid geworden op: 26 nov 2006, 00:41
Bericht
door Hugo » 10 nov 2007, 14:25
he thomas, volgens mij heb je het goed in de gaten. De vraag die jij stelt heeft maar een antwoord namelijk de kans op Verlies Verlies, Winst. In ieder ander geval speel je namelijk geen drie keer. Waarschijnlijk is de vraag wat de kans op winst is als je maximaal 3 keer speelt, dna is het inderdaad de kans op Winst + Verlies&Winst + Verlies&Verlies&Winst
dat verhaal van die binominaalcoefficient heb je hier helemaal niet nodig.
groetjes, namens WiFo, Hugo
I thought i was dead for a while, then I decided I was a lemon for a couple of weeks and I amused myself that time jumping in and out a gin tonic.
-
Thomas
- Gevorderde

- Berichten: 120
- Lid geworden op: 06 apr 2007, 02:02
Bericht
door Thomas » 10 nov 2007, 17:22
De reden waarom ik dit wilde weten is omdat ik online een spelletje speeld genaamd OGame. Hierbij kan je manen krijgen door grote slagen te maken waarbij puin vrijkomt. Je hebt daar tot maximaal 20% kans op een maan.
Ik had dus de discussie wat beter was. Één maal een poging van 20% of tot twee maal een poging van 10%. Bij de 10% zou je dus stoppen met proberen nadat je een maan had aangezien je één maan mag.
Ik had het volgende berekent:
Kans op een maan bij 20%:
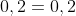
Kans op een maan bij tot twee pogingen met 10%:

Nu was er iemand die zei dat ik bij de laatste bereking ook
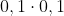
er bij moest tellen.