Zadeldak berekenen (hoeken)

[thisiseusch]

Ik wil het dak van mijn carport veranderen in een zadeldak.

De balken moeten daarvoor onder een hoek gezaagd gaan worden. Hierbij moet rekeningen gehouden worden met een overstek zodat de dakplaten boven de regengoot uitkomen. De metalen dakplaten hebben een lengte van 200 cm.

Hoe bereken ik de hoeken alfa en beta en de lengtes A, L, M, N?
.

[arie]

Kijk eerst naar rechthoekige driehoek PQR (rood):
\(PQ = B + J = 175.35 + 4.5 = 179.85\)
\(QR = 200\)
Dan is volgens de stelling van Pythagoras:
\(PQ^2 + PR^2 = QR^2\)
ofwel:
\(PR = \sqrt{QR^2 - PQ^2} = \sqrt{200^2 - 179.85^2} = 87.4870\)

\(\angle QPR = 90^o\)
\(\sin(\angle PQR) = \frac{PR}{QR}\)
dus
\(\angle PQR = \text{asin}\left( \frac{PR}{QR} \right) = \text{asin}\left( \frac{87.4870}{200} \right) = 25.9403^o\)
en omdat de som van de hoeken van elke driehoek \(180^o\) is, is
\(\angle PRQ = 180^o - \angle QPR - \angle PQR = 180^o - 90^o - 25.9403^o = 64.0597^o\)

De blauwe lijn ST loopt evenwijdig aan de rode lijn QR,
dus wegens F-hoeken geldt (zie bv. https://nl.wikipedia.org/wiki/F-_en_Z-hoeken) :
\(\beta = \angle PST = \angle PQR = 25.9403^o\)
en
\(\alpha = \angle PTS = \angle PRQ = 64.0597^o\)

Verder is
SV = TW = H = 11.7
en
\(\sin( \angle WRT) = \frac{TW}{RT}\)
dus
\(RT = \frac{TW}{\sin(\angle WRT)} = \frac{H}{\sin(\alpha)} = \frac{11.7}{\sin(64.0597^o)} = 13.0108\)

Tenslotte hebben we:
\(PT = PR - RT = 87.4870- 13.0108 = 74.4762\)


Zijn dit alle gegevens die je zocht?

[thisiseusch]

Bedankt zover echter is ik nog de afstanden L,N en M

[arie]

Nu ik er weer naar kijk blijkt je constructietekening niet te kloppen:
Als gegeven is dat PQ=179.85 en QR=200, dan moet PR=87.4870 zijn.
Hoeken alpha en beta blijven zoals we ze berekend hadden.
Met gegeven SQ = 11.8 + 4.5 = 16.3 geldt echter:
\(VS = SQ \cdot \sin(\beta) = 16.3 \cdot \sin(25.9403^o) = 7.13019\)
Dus H=VS kan nooit 11.7 zijn...

Dit is op te lossen door \(QR\) omhoog te schuiven naar \(Q_2R_2\).
De berekening moet in ieder geval aangepast worden.

Maar daarvóór moet je graag eerst nog even kijken hoe je de aansluiting van de staande balk (bruin) op de schuine balk (geel) wilt hebben.
Ik heb deze aansluiting in het plaatje horizontaal getekend, maar je kan ook denken aan schuin of trapsgewijs, afhankelijk van hoe je die balken aan elkaar wilt bevestigen en wat daarbij bouwkundig de meest solide optie is.

[arie]

In aanvulling op mijn vorige post:



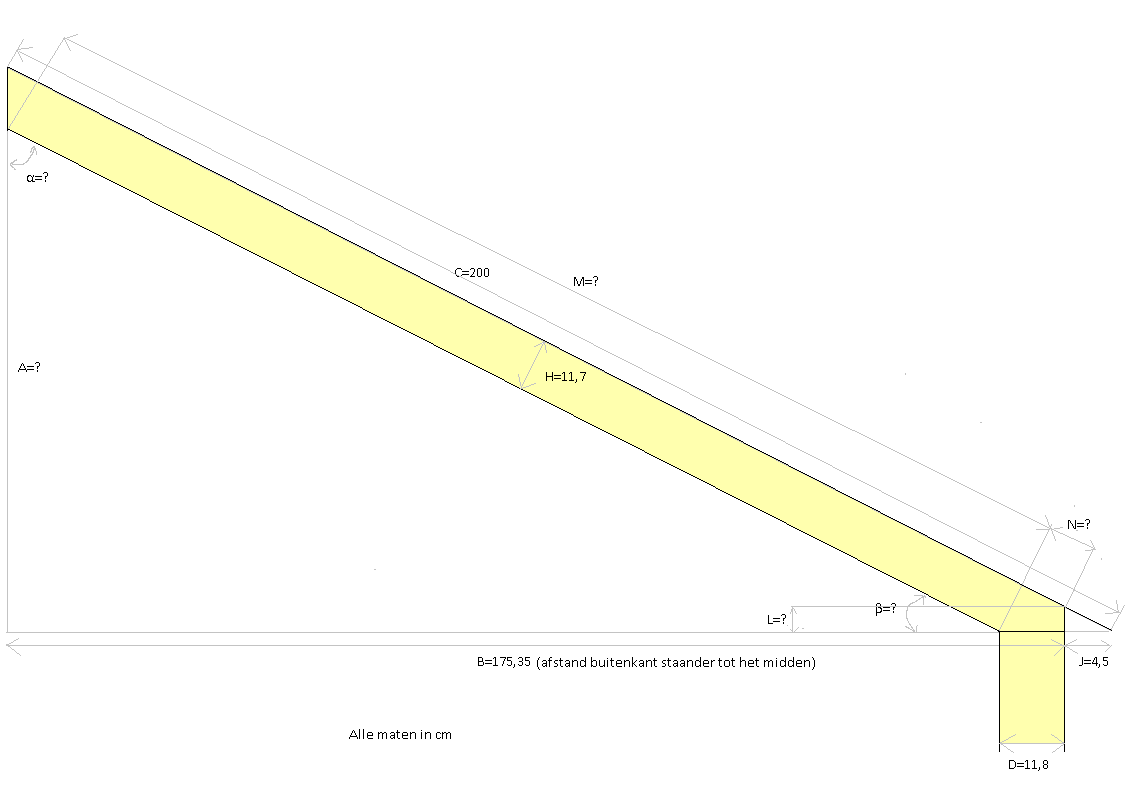
Hier de coordinaten van de punten in bovenstaand plaatje:
O = ( 0.00000000, 0.00000000 )
S = ( 163.55000000, 0.00000000 )
T = ( 0.00000000, 79.55797069 )
Z = ( -5.11799028, 82.04758806 )
R = ( 0.00000000, 92.56881306 )
W = ( 5.11799028, 90.07919569 )
V = ( 168.66799028, 10.52122500 )
M = ( 175.35000000, 7.27079924 )
K = ( 178.21006692, 5.87953589 )
H = ( 175.35000000, 0.00000000 )
L = ( 173.09207664, -4.64168911 )
J = ( 179.85000000, 0.00000000 )
Q = ( 179.85000000, 5.08179974 )

en hier enkele afstanden:
OT = 79.557971
OS = 163.55000
ST = 181.87378
TZ = 5.6913987
ZR = 11.700000
RW = 5.6913987
WV = 181.87378
VM = 7.4306474
MK = 3.1805026
MH = 7.2707992
KQ = 1.8236676
KH = 6.5382662
HL = 5.1617338
LS = 10.611150
SH = 11.800000
HJ = 4.5000000
JQ = 5.0817997
QR = 200.00000


waarbij voor de afstand \(AB\) tussen punten \(A=(a_x, a_y)\) en \(B=(b_x, b_y)\) geldt:

\(AB = \sqrt{(a_x-b_x)^2 + (a_y-b_y)^2}\)

[thisiseusch]

Bedankt daarvoor. Hoe heb jij nu het een en ander berekent? Is interessant te weten als er een maat wijzigt (bijvoorbeed de breedte van de dakgoot en dus de overstek).
Welk programma heb je gebruikt om de constructie tekening te maken?
Het is inderdaad de constructie waarna ik op zoek ben. Ik had zelf al gerekend en gezaag maar toen was dit het resultaat:

Terwijl ik iets als dit moet hebben:

[arie]

De berekeningen heb ik gemaakt zoals in mijn eerste post met de basisformules voor rechthoekige driehoeken.
Voor een rechthoekige driehoek met rechthoekszijden \(a\) en \(b\), schuine zijde \(c\) en \(\gamma = \angle ACB = 90^o\) gelden:

- de stelling van Pythagoras:
\(a^2 + b^2 = c^2\)

- en de hoekformules:
\(\sin(\alpha) = \frac{\text{overstaande zijde}}{\text{schuine zijde}}\)
\(\cos(\alpha) = \frac{\text{aanliggende zijde}}{\text{schuine zijde}}\)
\(\tan(\alpha) = \frac{\text{overstaande zijde}}{\text{aanliggende zijde}}\)

De formule voor de afstand tussen 2 punten A en B heb ik in mijn vorige post al gegeven.


Mijn resultaten heb ik geplot via een programmeerpakket. Veel programmeertalen bieden die mogelijkheid.

Om het tekenen te combineren met het rekenwerk wordt GeoGebra nogal eens gebruikt:
https://www.geogebra.org/?lang=en
Via de knop "START REKENMACHINE"
kom je in het scherm "Grafisch rekenen",
klik je in de linker balk van dat scherm op "Knoppen" dan verschijnen een heleboel knoppen voor verschillende constructie-elementen, zoals snijpunten vinden, hoeken meten, lijnen tekenen, raaklijnen maken, spiegelingen etc.

Er bestaan ook pakketten voor constructie-tekenen en Computer Aided Design, maar daar weet ik onvoldoende van af om zinnige adviezen over te kunnen geven.

[thisiseusch]

Super bedankt. Fijn dat het mensen zoals jij geeft die zich de tijd en moeite nemen.