Noem:
x = hoeveelheid van het eerste mengsel, en
y = hoeveelheid van het tweede mengsel.
(neem impliciet aan: x >= 0 en y >= 0: we kunnen immers geen negatieve hoeveelheden kopen)
Kijk dan naar de componenten, te beginnen met component A:
Daarvoor moet gelden:
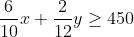
De vergelijking van de lijn die dit gebied begrenst is:
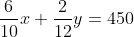
Het snijpunt van deze lijn met de y-as vind je door x=0 te stellen: dan is y = 2700
Het snijpunt van deze lijn met de x-as vind je door y=0 te stellen: dan is x = 750
De hoeveelheden x en y moeten dus op of boven deze lijn liggen: het groene gebied in onderstaand plaatje:

Bepaal op dezelfde manier de eisen aan x en y op grond van component B en component C.
Je krijgt dan een plaatje als hieronder.
Wat zijn de vergelijkingen van de 2 nieuwe lijnen die je zo vindt?

Bepaal vervolgens de coördinaten van de hoekpunten P, Q, R en S die het groene gebied begrenzen:

Kijk tenslotte naar de kosten:
x kost 1.50 per kg
y kost 3.75 per kg
dus

Dit is voor elke vaste prijs ook weer de vergelijking van een lijn.
Net als hierboven kunnen we nu in de grafiek voor elke prijs aangeven hoeveel x en/of y we kunnen kopen.
Voorbeeld:
prijs = 300 euro:
als x = 0 is y = 300/3.75 = 80
als y = 0 is x = 300/1.5 = 200
Het lijnstuk van (0,80) tot (200,0) geeft de hoeveelheden x en y aan die we voor 300 euro kunnen kopen.
Hoe hoger het bedrag, hoe meer we kunnen kopen.
Hieronder in rood aangegeven: 300 euro, 1200 euro en 2400 euro:

De vraag is dan:
voor welke prijs raakt de bijbehorende rode lijn voor het eerst de rand van het groene gebied?
(Noot: het is te bewijzen dat voor dit soort problemen de hoekpunten een (van de) oplossing leveren, we hoeven dus in feite alleen de kosten van de punten P, Q, R en S te bepalen en daaruit de laagste te kiezen).






