Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Matrixrekenen, vectorruimten, groep-en ringstructuren, (lineaire) tranformaties.
-
grades
- Nieuw lid

- Berichten: 11
- Lid geworden op: 09 nov 2011, 15:47
Bericht
door grades » 01 feb 2012, 14:02
Wie snapt deze:
Laat zien dat de functie f(x) = (x² + x -

/(x - 1) ook geschreven kan worden als f(x) = 2x + 3 - 5/(x - 1)
Ik snap niet hoe je dit zo kan schrijven, Waarschijnlijk zie ik iets over het hoofd maar het hoort bij een hoofdstuk over staartdeling en heb het hier al mee proberen op te lossen maar ik kom niet van de ene op de ander.
-
barto
- Vergevorderde

- Berichten: 654
- Lid geworden op: 07 jun 2011, 16:02
Bericht
door barto » 01 feb 2012, 14:06
grades schreef:Wie snapt deze:
Laat zien dat de functie f(x) = (x² + x -

/(x - 1) ook geschreven kan worden als f(x) = 2x + 3 - 5/(x - 1)
Ik snap niet hoe je dit zo kan schrijven, Waarschijnlijk zie ik iets over het hoofd maar het hoort bij een hoofdstuk over staartdeling en heb het hier al mee proberen op te lossen maar ik kom niet van de ene op de ander.
(Om even de smiley weg te werken)
 = \frac{x^2 + x - 8}{x - 1})
Kun je de staartdeling volgens euclides uitvoeren, of eventueel met Horner.?
Euclides:
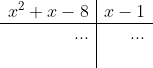
Horner:
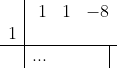
Laatst gewijzigd door
barto op 01 feb 2012, 14:34, 5 keer totaal gewijzigd.
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.
-
op=op
- Vergevorderde

- Berichten: 1087
- Lid geworden op: 23 apr 2010, 18:11
Bericht
door op=op » 01 feb 2012, 14:31
Dat klopt ook niet.
 = \frac{x^2 + x - 8}{x - 1})
De teller is niet door de noemer deelbaar, want dan zou x=1 niet alleen een nulpunt van de teller zijn, maar ook van de noemer.
De breuk
 = \frac{x^2 + x - 2}{x - 1})
kan daarom wel vereenvoudigd worden, dus
 = \frac{x^2 + x - 8}{x - 1} = \frac{x^2 + x - 2}{x - 1} -\frac{6}{x-1})
,
waarbij je de eerste breuk nog moet vereenvoudigen.
-
barto
- Vergevorderde

- Berichten: 654
- Lid geworden op: 07 jun 2011, 16:02
Bericht
door barto » 01 feb 2012, 14:37
op=op schreef:Dat klopt ook niet.
Hoezo?
De teller hoeft niet deelbaar te zijn door de noemer.
Bij beide rekenschema's kun je quotiënt
)
en rest
)
aflezen.
Dan stel je gewoon:
=q(x)+\frac{r(x)}{x-1})
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.
-
grades
- Nieuw lid

- Berichten: 11
- Lid geworden op: 09 nov 2011, 15:47
Bericht
door grades » 01 feb 2012, 14:52
Oke. Bedankt.
Maar wat ik nog niet snap is hoe je uit de ene formule de andere krijgt of dat ze gelijk zouden zijn.
-
op=op
- Vergevorderde

- Berichten: 1087
- Lid geworden op: 23 apr 2010, 18:11
Bericht
door op=op » 01 feb 2012, 15:04
barto schreef:op=op schreef:Dat klopt ook niet.
Hoezo?
De teller hoeft niet deelbaar te zijn door de noemer.
Bij beide rekenschema's kun je quotiënt
)
en rest
)
aflezen.
Dan stel je gewoon:
=q(x)+\frac{r(x)}{x-1})
Je aanvulling kwam na mijn bijdrage en sloeg dus niet op jouw reactie, maar op het feit dat de uitkomst niet f(x) = 2x + 3 - 5/(x - 1) is.
Dat deze uitkomst niet klopt kun je nagaan door een waarde in te vullen, b.v. x=2.
-
barto
- Vergevorderde

- Berichten: 654
- Lid geworden op: 07 jun 2011, 16:02
Bericht
door barto » 01 feb 2012, 15:06
Je hebt:
=\frac{x^2+x-8}{x-1})
Stel je nu
=x^2+x-8)
, het deeltal.
En:
=x-1)
, de deler.
Dan staat er:
=\frac{D(x)}{d(x)})
Net zoals bij getallen kan een deling geschreven worden als quotiënt en rest.
Neem de deling
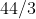
. Het deeltal (D) is 44. De deler (d) is 3.
Het quotiënt (q) is 14. De rest (r) is 2.
We schrijven:
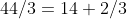
of algemeen:
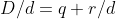
Bij functies gaat het net hetzelfde:
=\frac{D(x)}{d(x)}=q(x)+\frac{r(x)}{d(x)})
Het quotiënt en de rest bepaal je met de deling volgens Euclides of Horner.
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.
-
David
- Moderator

- Berichten: 4927
- Lid geworden op: 14 mei 2009, 16:22
Bericht
door David » 01 feb 2012, 15:09
Grades, bedoel je:
=\frac{2x^2+x-8}{x-1})
Dat komt overeen met je antwoord.
Een derde methode is:
(ax + b)(x - 1) + c = 2x^2 + x - 8
Haakjes wegwerken en oplossen van links naar rechts. Dan door (x - 1) delen.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 01 feb 2012, 15:31
Wat denk je van:
=\frac{x^2+x-8}{x-1}=\frac{x(x-1)+x+x-8}{x-1}=\frac{x(x-1)+2(x-1)+2-8}{x-1}=...)
Wat is de gedachtegang?
Merk op dat dit niet klopt met je (gegeven) antwoord ...
-
grades
- Nieuw lid

- Berichten: 11
- Lid geworden op: 09 nov 2011, 15:47
Bericht
door grades » 01 feb 2012, 16:09
Wat ik niet snap is dat er in het boek word beweerd.
dat je:
f(x) = (x² + x -

/(x - 1)
ook kunt schrijven als:
f(x) = 2x + 3 - 5/(x - 1)
hoe ik de bovenste formule ook bereken, ik krijg de onderste er niet uit.
En zie dus niet hoe dit zou kunnen kloppen.
-
grades
- Nieuw lid

- Berichten: 11
- Lid geworden op: 09 nov 2011, 15:47
Bericht
door grades » 01 feb 2012, 16:11
poppetje moet zijn 8 )
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 09 mar 2012, 10:02
grades schreef:Wat ik niet snap is dat er in het boek word beweerd.
dat je:
f(x) = (x² + x -

/(x - 1)
ook kunt schrijven als:
f(x) = 2x + 3 - 5/(x - 1)
hoe ik de bovenste formule ook bereken, ik krijg de onderste er niet uit.
En zie dus niet hoe dit zou kunnen kloppen.
Ben je er al uit ...




