Volume van een bol
-
grassprietje
- Nieuw lid

- Berichten: 5
- Lid geworden op: 27 dec 2013, 22:47
Volume van een bol
Hallo
Oké ik wil dus het volume van een bol berekenen via een enkelvoudige integraal. Dus een Riemannsom van on. kleine cirkels. Maar ik raak vast; ik zal een foto bijvoegen zodat je ziet waar ik vastloop.
Kan iemand mij een hint geven hoe ik verder moet ;of wat ik fout doe?
hier is de URL: https://imageshack.com/i/g9e3e9j
Oké ik wil dus het volume van een bol berekenen via een enkelvoudige integraal. Dus een Riemannsom van on. kleine cirkels. Maar ik raak vast; ik zal een foto bijvoegen zodat je ziet waar ik vastloop.
Kan iemand mij een hint geven hoe ik verder moet ;of wat ik fout doe?
hier is de URL: https://imageshack.com/i/g9e3e9j
Re: Volume van een bol
Kan je r² uitdrukken in x?
(hint: r = y)
(hint: r = y)
-
grassprietje
- Nieuw lid

- Berichten: 5
- Lid geworden op: 27 dec 2013, 22:47
Re: Volume van een bol
wel ik dacht het volume van een cilinder (pi)r²h
met h=dx en me straal r
dan geeft dV = π x² dx toch niet het volume van die schijf?
met h=dx en me straal r
dan geeft dV = π x² dx toch niet het volume van die schijf?
Re: Volume van een bol
Je tekent in een xy-stelsel, dwz je moet y uitdrukken in x.
Bedenk dat de straal van je cirkelschijf(je) niet r is maar y die behoort bij je x ...
Ken je de functie die behoort bij een halve cirkel (boven de x-as), zoals je getekend hebt?
Je wilt het volume berekenen mbv een omwentelingslichaam, klopt dat?
De (bepaalde) integraal die daarbij hoort is (grenzen nog in te vullen):
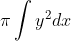
Komt dit je bekend voor ...
Bedenk dat de straal van je cirkelschijf(je) niet r is maar y die behoort bij je x ...
Ken je de functie die behoort bij een halve cirkel (boven de x-as), zoals je getekend hebt?
Je wilt het volume berekenen mbv een omwentelingslichaam, klopt dat?
De (bepaalde) integraal die daarbij hoort is (grenzen nog in te vullen):
Komt dit je bekend voor ...
-
grassprietje
- Nieuw lid

- Berichten: 5
- Lid geworden op: 27 dec 2013, 22:47
Re: Volume van een bol
@safex: ik heb em al eens opgelost via omwentelingslichaam daar gebruikte ik y=(R²-x²)^1/2
Hier wil ik hem dus oplossen adhv oneindig veel cilinder oppervlakken.
en zoals arie zegt: hier is y=r dus r=y=(R²-x²)^1/2
als ik dat invul in mijn integraal dV kom ik idd uit op het bekende 3/4(pi)r³
Het was eigenlijk redelijk eenvoudig merci
Hier wil ik hem dus oplossen adhv oneindig veel cilinder oppervlakken.
en zoals arie zegt: hier is y=r dus r=y=(R²-x²)^1/2
als ik dat invul in mijn integraal dV kom ik idd uit op het bekende 3/4(pi)r³
Het was eigenlijk redelijk eenvoudig merci
Re: Volume van een bol
Mooi!
Je weet (misschien) ook dat je de grenzen 0 en R kan gebruiken? Zo ja, waarom?
Je weet (misschien) ook dat je de grenzen 0 en R kan gebruiken? Zo ja, waarom?
-
grassprietje
- Nieuw lid

- Berichten: 5
- Lid geworden op: 27 dec 2013, 22:47
Re: Volume van een bol
ja door symmtrie kan je gewoon van 0 tot R integreren maal 2
Re: Volume van een bol
Ok! Succes verder.
Achteraf gezien, heb ik je probleem niet begrepen ...
Achteraf gezien, heb ik je probleem niet begrepen ...
-
grassprietje
- Nieuw lid

- Berichten: 5
- Lid geworden op: 27 dec 2013, 22:47
Re: Volume van een bol
ik had eigenlijk gewoon een verband nodig tussen de grote R en de kleine r.
enfin deze oef is idd wel gemakkelijker door een omwentelingslichaam te gebruiken.
ik wou het ook eens oplossen zonder gebruik te maken van een omwentelingslichaam.
enfin deze oef is idd wel gemakkelijker door een omwentelingslichaam te gebruiken.
ik wou het ook eens oplossen zonder gebruik te maken van een omwentelingslichaam.
